树
基本概念
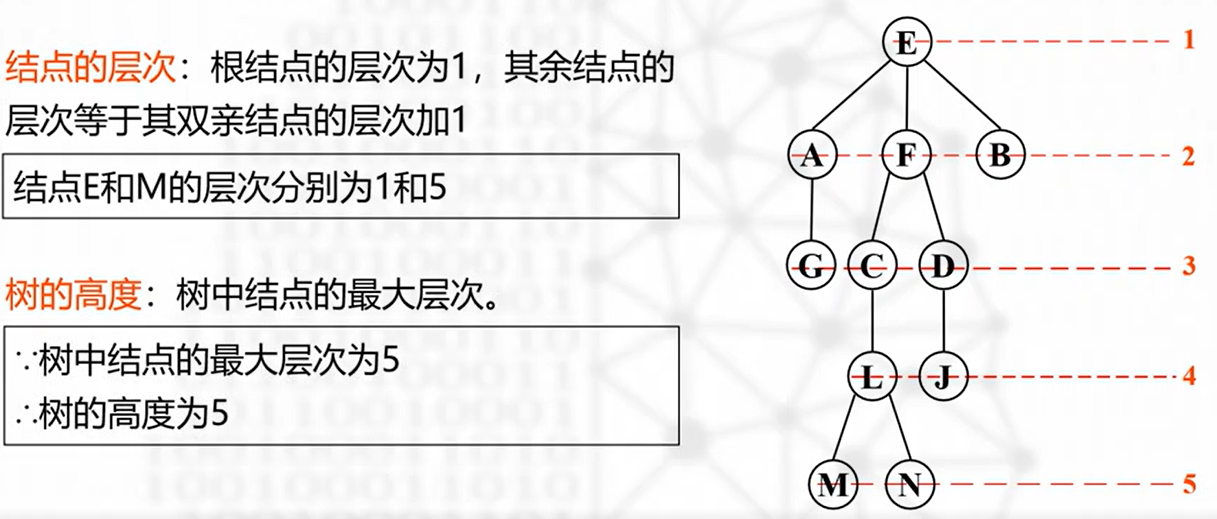
结点的度:结点拥有的子树数
树的度:树中各结点度的最大值(下图中为3)

无序树:树中结点的各子树之间的顺序无关,可以交换位置
有序树:树中结点的各棵子树从左到右顺序相关,交换任意两棵子树的位置都将改变原来树的结构
森林:树的集合,0棵或多棵不相交的树组成森林
二叉树
二叉树的五种基本形态
注:在二叉树中结点的子树要区分左右子树,并非无序;二叉树的每个结点最多只能有2棵子树

性质:
- 二叉树的第 i(i>=1)层上至多有 2i-1 个结点
- 高度为 h 的二叉树上至多有 2h-1 个结点
- 包含 n 个结点的二叉树的高度最矮为 log2(n+1) 向上取整,最高为 n
- 当每一层都只有一个结点的时候,二叉树高度最高,为 n
- 任一二叉树中,若叶结点数量为 n0,度为 2 的结点数量为 n2,则有 n0=n2+1
满二叉树
高度为 h,且有 2h-1 个结点的二叉树(每一层结点数量都饱和)
满二叉树一定是完全二叉树,也是扩充二叉树
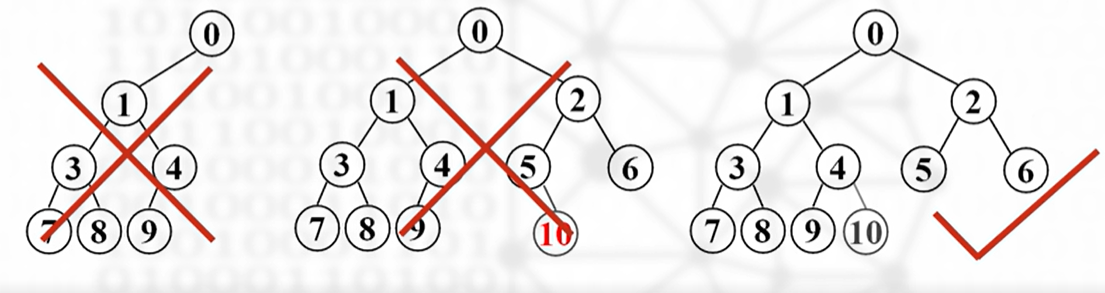
完全二叉树
- 只有最下面两层结点的度可以小于 2,其它层中的结点的度均等于 2
- 最下一层的叶结点均依次集中在靠左的若干位置上
- 具有 n 个结点的完全二叉树的高度为 log2(n+1) 向上取整
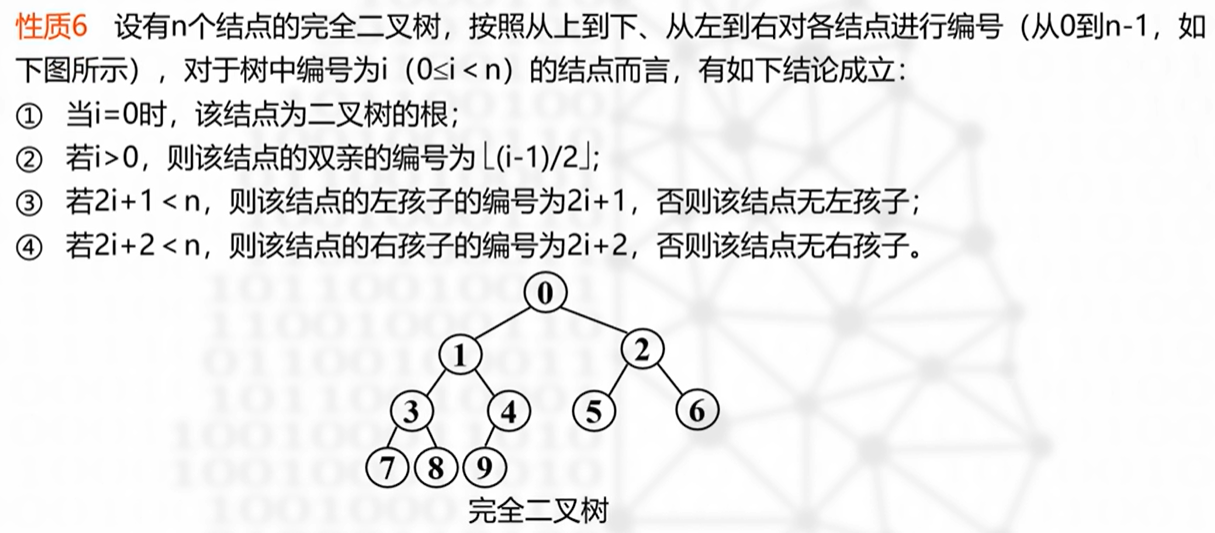
扩充二叉树(2-树)
除叶子结点以外,其余结点都必须有 2 个孩子(仅存在度为 2 和 0 的结点,不存在度为 1 的结点)
求二叉树的结点总数量
$$
二叉树的结点总数量 = 左子树结点总数量 + 右子树结点总数量 + 根节点
$$
简单代码实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
| #include <iostream>
struct TreeNode {
int val;
TreeNode* left;
TreeNode* right;
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};
int countNodes(TreeNode* root) {
if (root == nullptr) {
return 0;
}
return 1 + countNodes(root->left) + countNodes(root->right);
}
int main() {
TreeNode* root = new TreeNode(1);
root->left = new TreeNode(2);
root->right = new TreeNode(3);
root->left->left = new TreeNode(4);
root->left->right = new TreeNode(5);
int totalNodes = countNodes(root);
std::cout << "二叉树的节点总数: " << totalNodes << std::endl;
delete root->left->left;
delete root->left->right;
delete root->left;
delete root->right;
delete root;
return 0;
}
|
清空二叉树
关键代码实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| void TreeClear(BinaryTree *bt)
{
Clear(bt->root);
}
void Clear(BTNode *t)
{
if(!t)
return;
Clear(t->leftChild);
Clear(t->rightChild)l
free(t);
}
|
二叉树的遍历
先序遍历(深度优先)—— O(n)
先访问根结点,再依次遍历左右子树
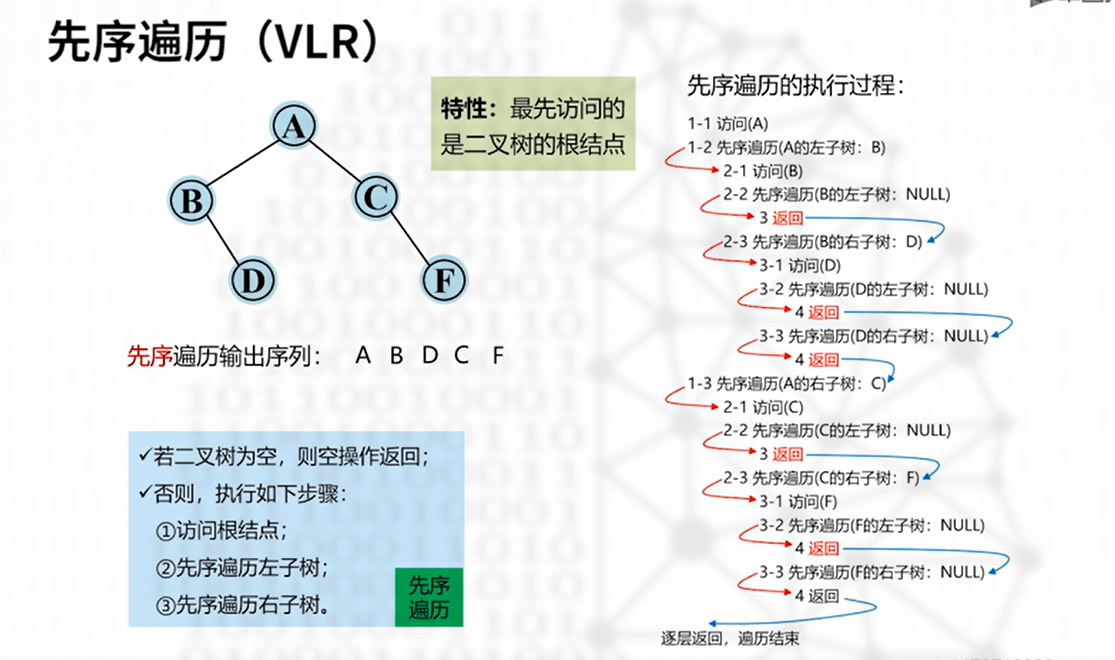
关键代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
| void PreOrderTree(BinaryTree *bt)
{
PreOrder(bt->root);
}
void PreOrder(BTNode *t)
{
if(!t)
return;
printf("%c",t->element);
PreOrder(t->lChild);
PreOrder(t->rChild);
}
|
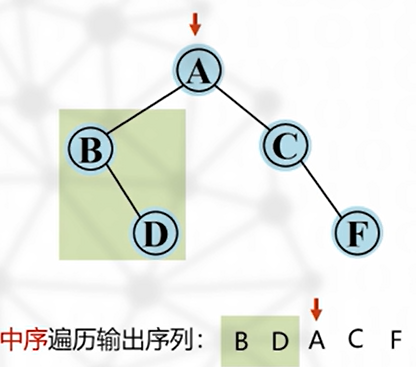
中序遍历(深度优先)—— O(n)
先遍历左子树,再访问根节点,最后遍历右子树
特性:根节点左子树中所有结点先于根结点访问输出,而右子树所有结点在根结点之后访问输出
关键代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
| void InOrderTree(BinaryTree *bt)
{
InOrder(bt->root);
}
void InOrder(BTNode *t)
{
if(!t)
return;
InOrder(t->lChild);
printf("%c",t->element);
InOrder(t->rChild);
}
|
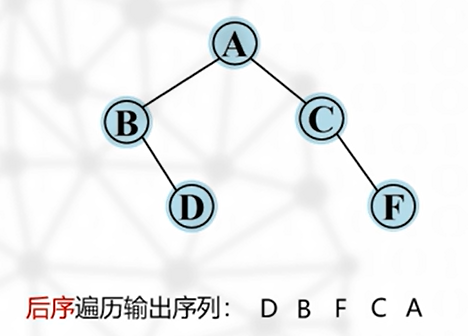
后序遍历(深度优先)—— O(n)
先依次遍历左右子树,最后访问根结点
特性:最后访问输出的是该二叉树的根结点
关键代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
| void PostOrderTree(BinaryTree *bt)
{
PostOrder(bt->root);
}
void PostOrder(BTNode *t)
{
if(!t)
return;
PostOrder(t->lChild);
PostOrder(t->rChild);
printf("%c",t->element);
}
|
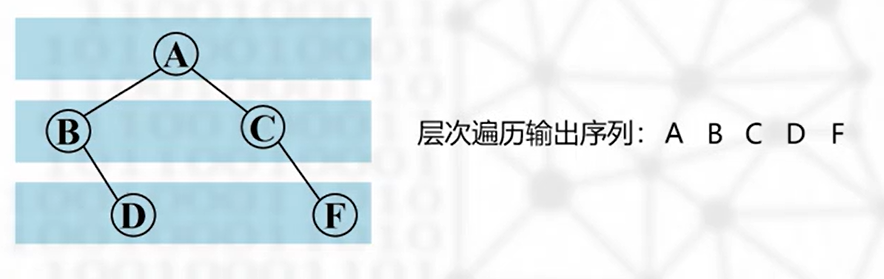
层次遍历(宽度优先)
从上到下、从左到右逐层访问二叉树每一个结点,每个结点访问且仅访问一次(非递归)
关键代码——时间复杂度 O(n):
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| #define QueueSize 100
void LevelOrderTree(BinaryTree *tree) {
Queue Q;
BTNode *p;
if(!tree->root)
return;
Create(&Q, QueueSize);
Enqueue(&Q, tree->root);
while(!isEmpty(&Q)){
Front(&Q, &p);
DeQueue(&Q);
printf("%c ", p->element);
if(p->leftChild)
Enqueue(&Q, p->leftChild);
if(p->rightChild)
Enqueue(&Q, p->rightChild);
}
Destroy(&Q);
}
|
二叉树遍历的相关性质
- 已知 先序和中序遍历,或者后序和中序遍历,可以唯一确定一棵二叉树
- 若二叉树中结点 n>1,在已知二叉树 先序和后序遍历 情况下,无法唯一确定一棵二叉树
先序+中序

后序+中序

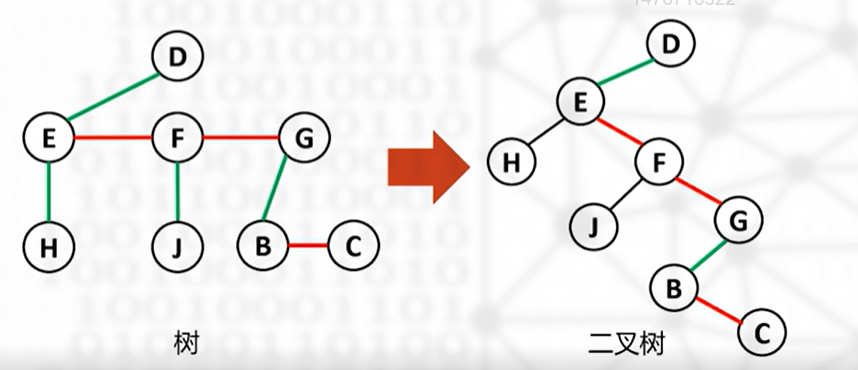
树转化为二叉树
将一棵树转换生成二叉树,则生成的二叉树的根结点一定没有右子树
转换方法:

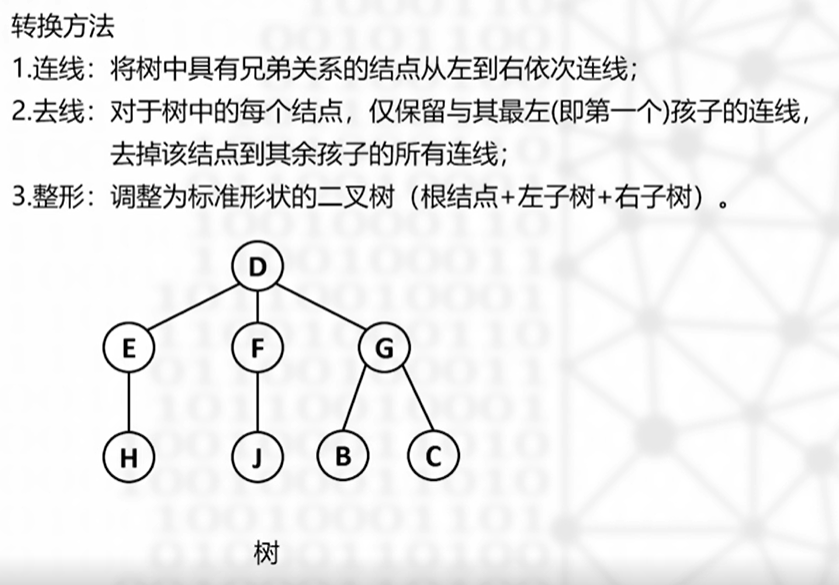
首先连线,并断去除最左的线(之前补的不动)
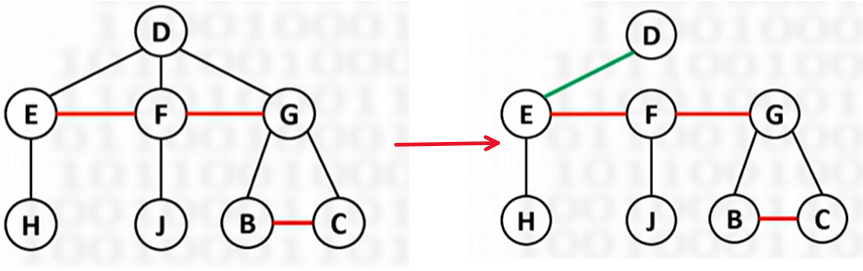
横右竖左
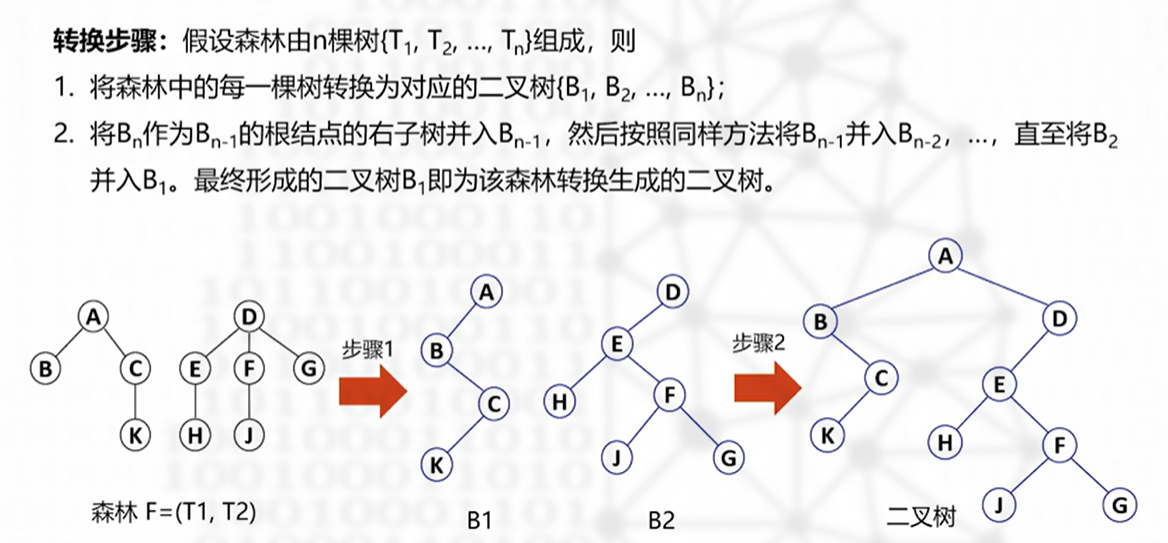
森林转换为二叉树
二叉树到树/森林
二叉树到树
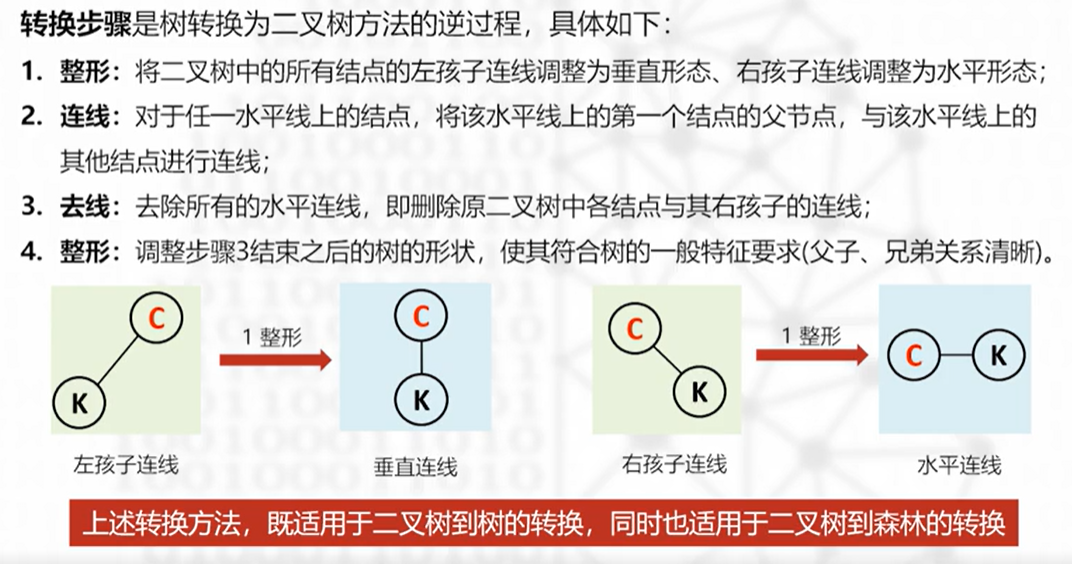
具体转化流程如下:
- 首先区分左右结点连线
- 同一水平线上的结点与上位结点连线
- 去除横线
- 调整形态
.png)
性质
- 如果二叉树只存在左子树,则可以转化成树;如果二叉树还存在右结点,则可以转化为包含多棵树的森林
- 二叉树中的左孩子转换后保持原父子关系;右孩子与原父结点变为兄弟关系
二叉树到森林
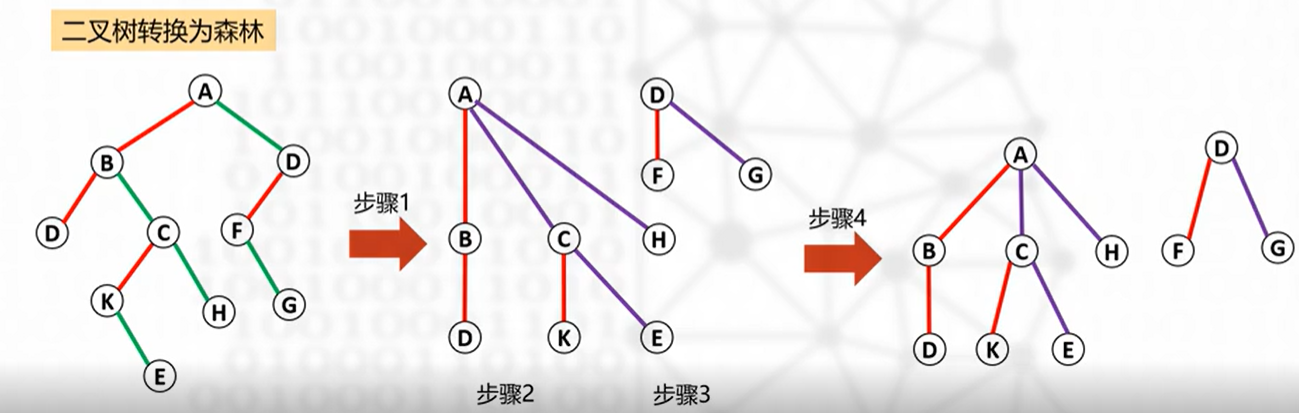
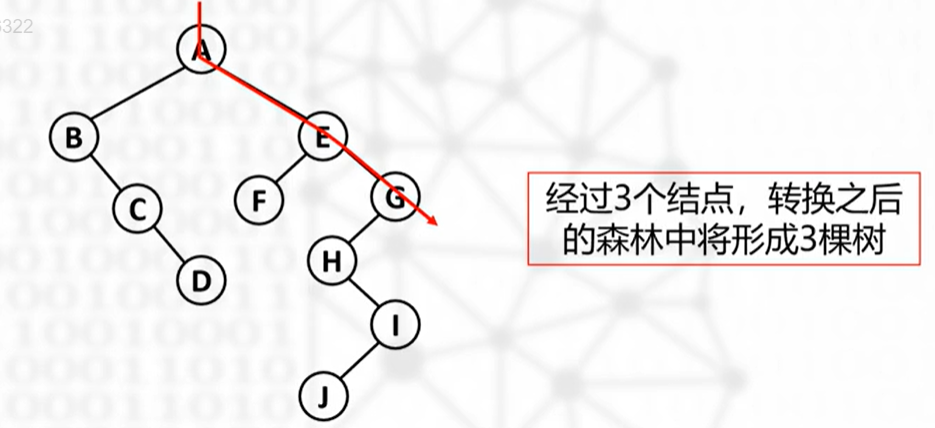
怎么判断一棵二叉树转换后包含几棵树
如下图画一根线,有多少右结点,转换后就有多少棵树
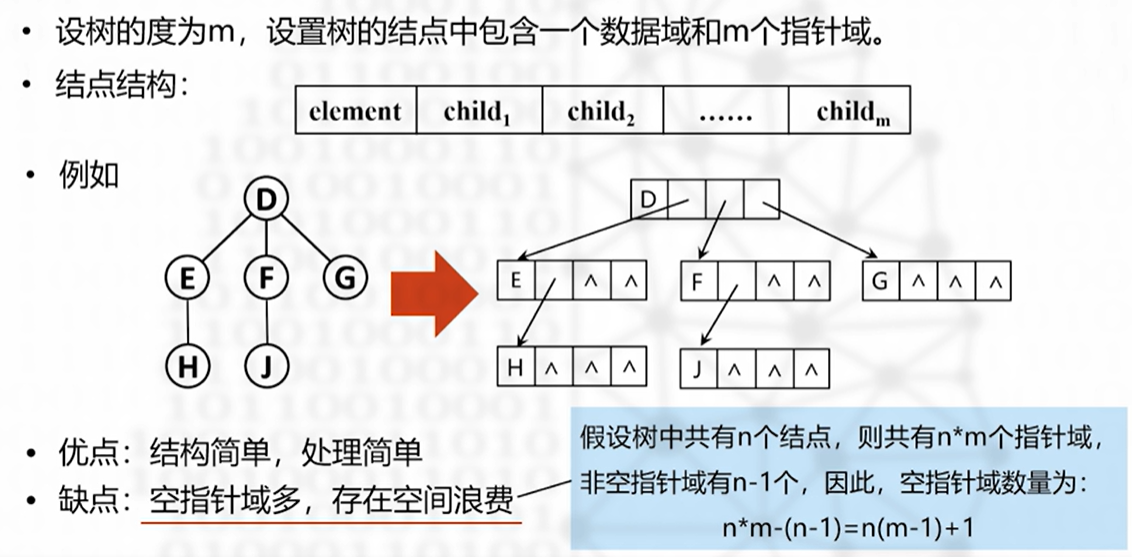
树和森林的存储表示
多重链表表示法
孩子兄弟表示法
利用 树/森林 与 二叉树 之间的对应关系
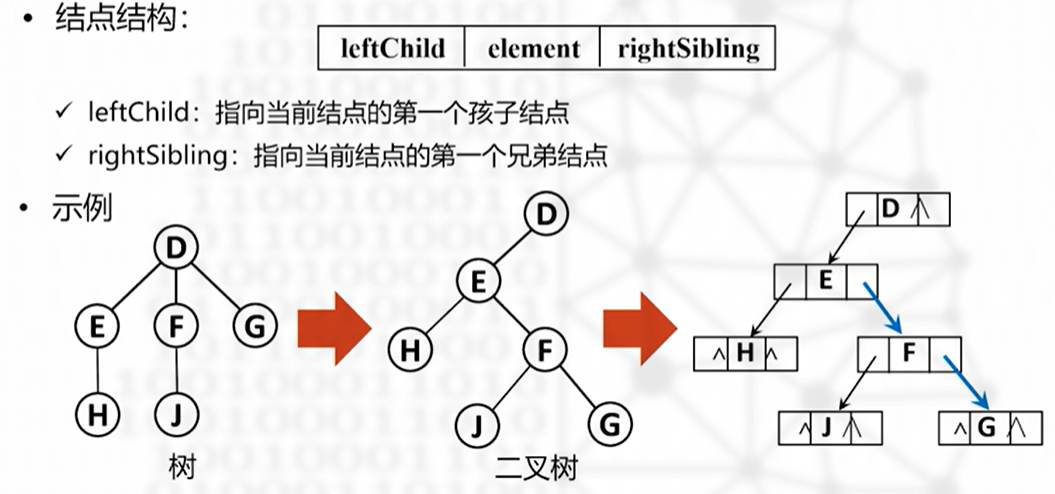
优点:能够继承二叉树的二叉链表的部分结构特性,以及部分运算操作
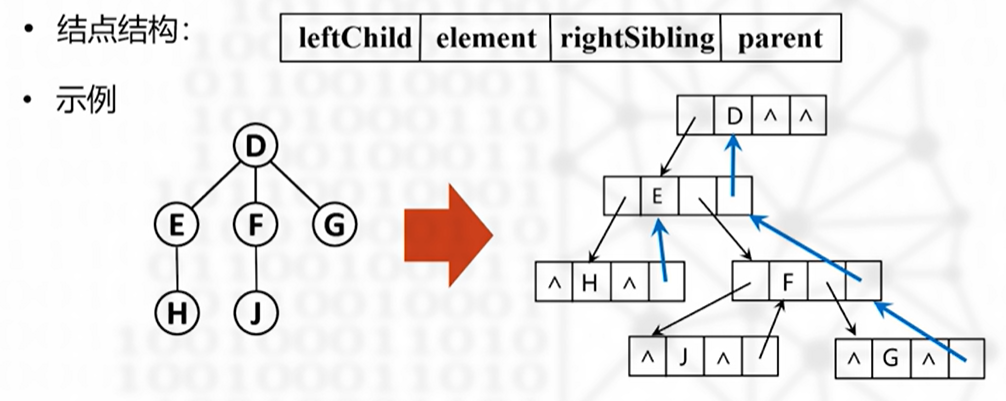
三重链表表示法
优点:能够方便访问结点的双亲和孩子
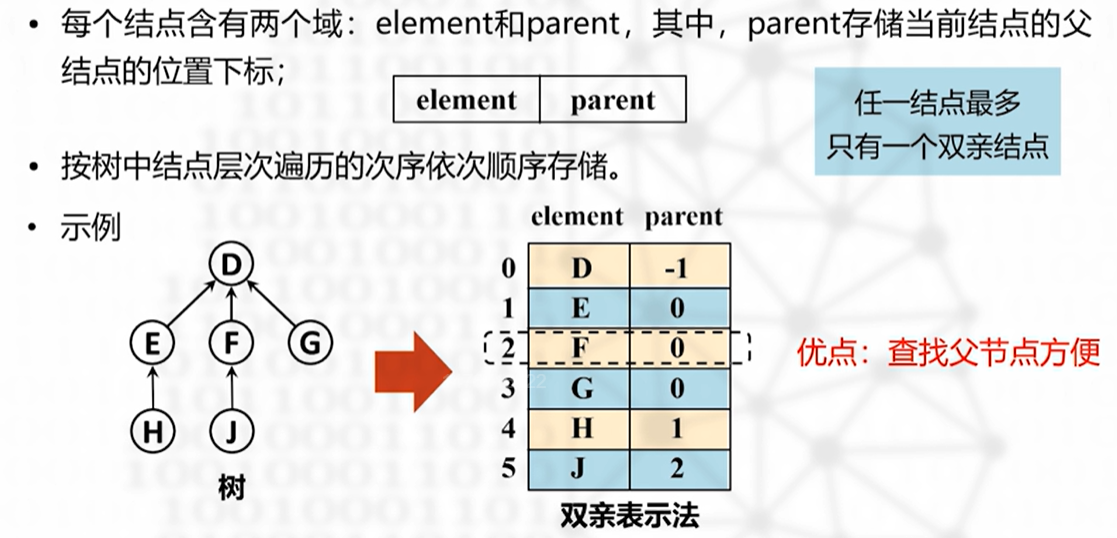
双亲表示法(顺序)
缺点:不方便从父结点到孩子结点的查找
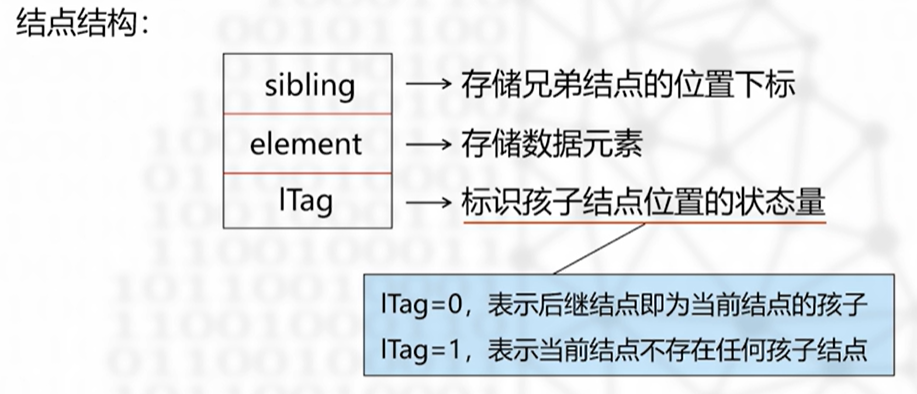
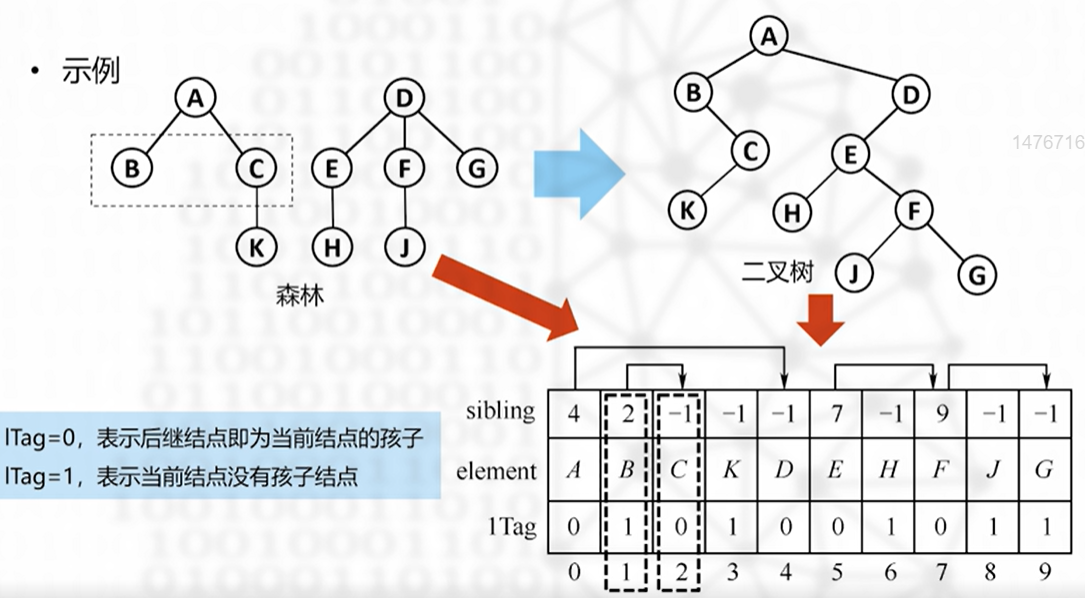
带右链的先序表示法(顺序)
结点存储顺序:按照对应的二叉树的先序遍历的顺序存储
树和森林的遍历
先序遍历
- 访问第一棵树的根
- 第一棵树根结点的子树构成的森林
- 其余树
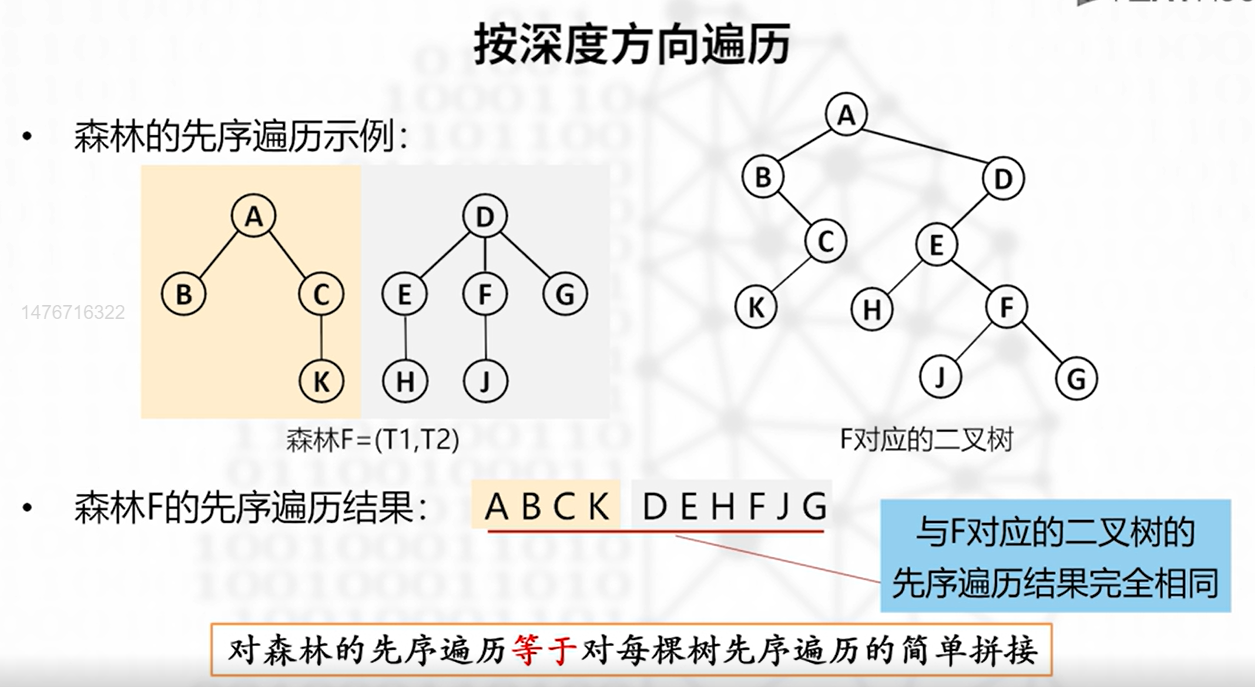
中序遍历
- 第一棵树根结点的子树构成的森林
- 访问第一棵树的根
- 其余树
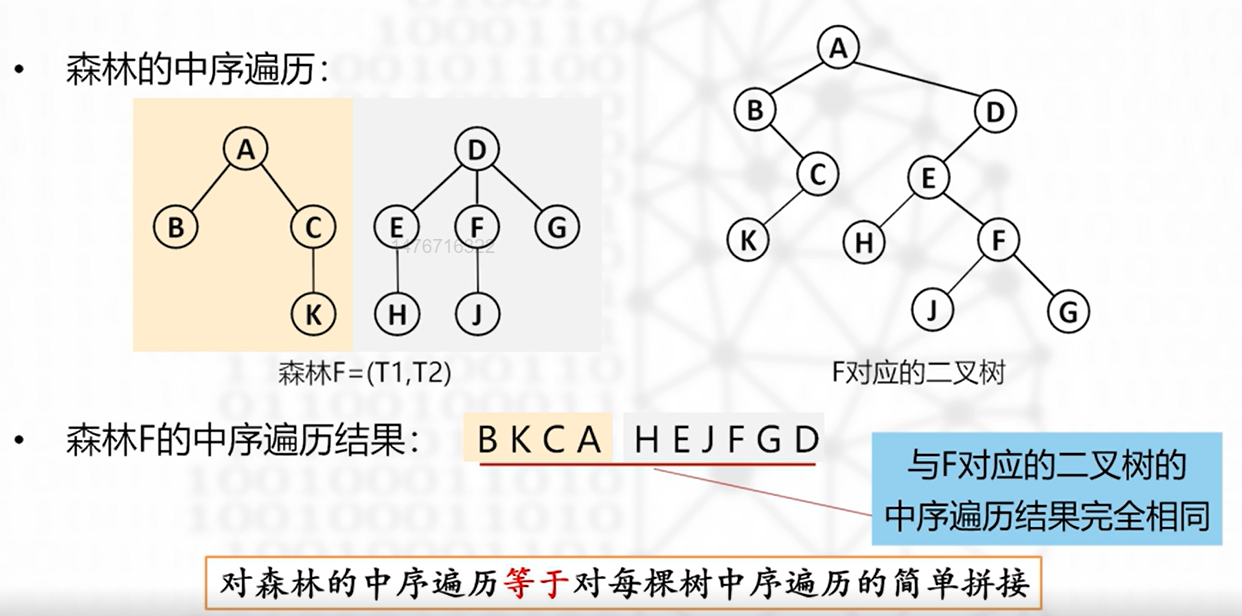
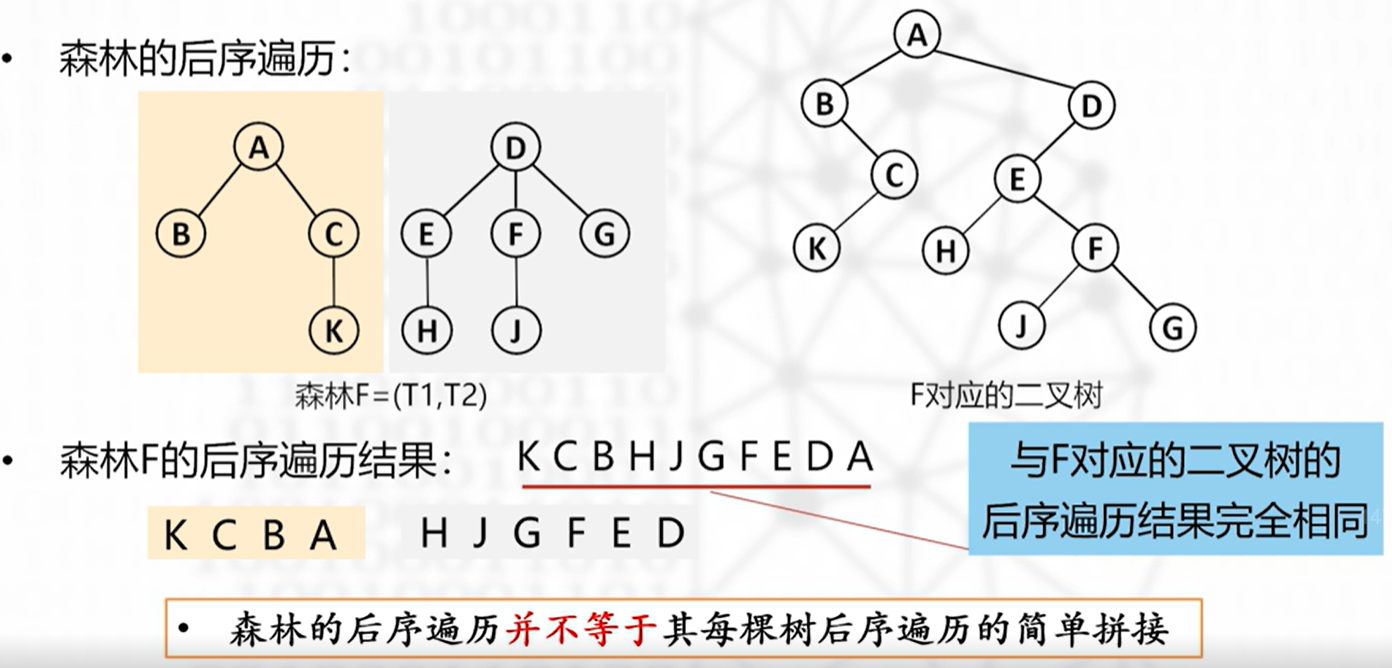
后序遍历
- 第一棵树根结点的子树构成的森林
- 其余树
- 访问第一棵树的根
第一棵树的根结点被第二棵树分隔,对根结点的访问被推迟到树上所有结点都访问完毕才进行——>逻辑上不自然
层次遍历
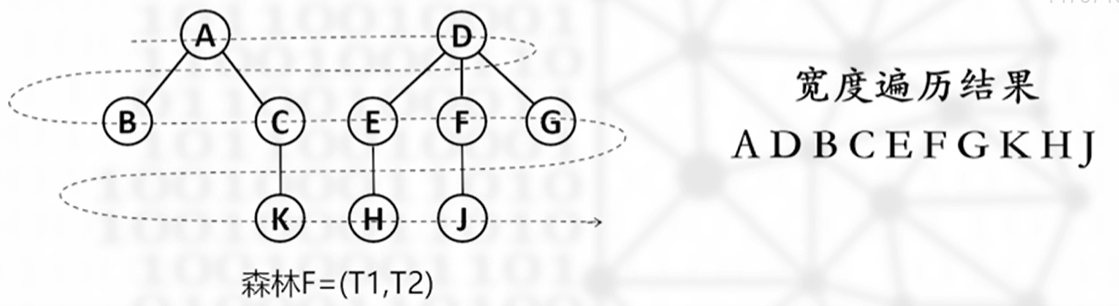

















.png)











