哈夫曼树
哈夫曼树
树的路径长度
结点的路径长度:从根结点到该结点的路径上所包括的边的数目
树的内路径长度
除叶结点外,从根到树中其他所有结点的路径长度之和
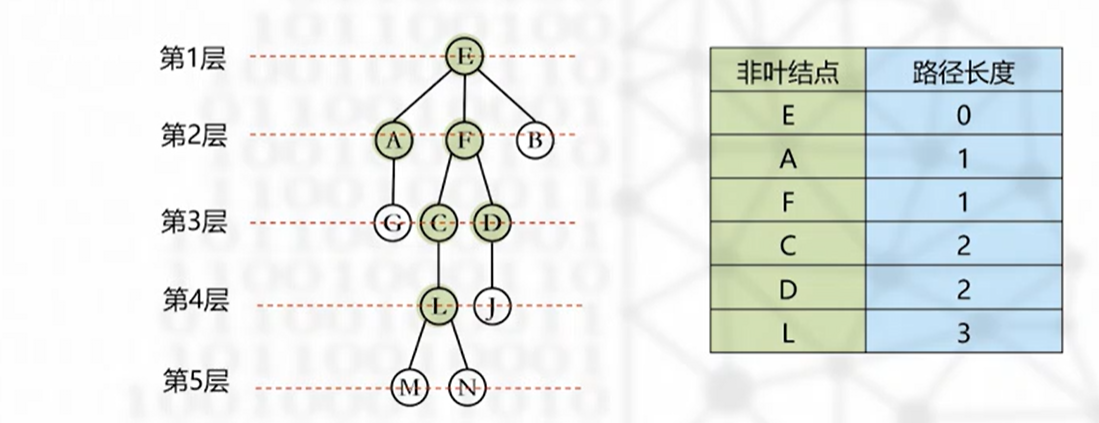
树的内路径长度=1+1+2+2+3=9
树的外路径长度
从根结点到树中所有叶子结点的路径长度之和
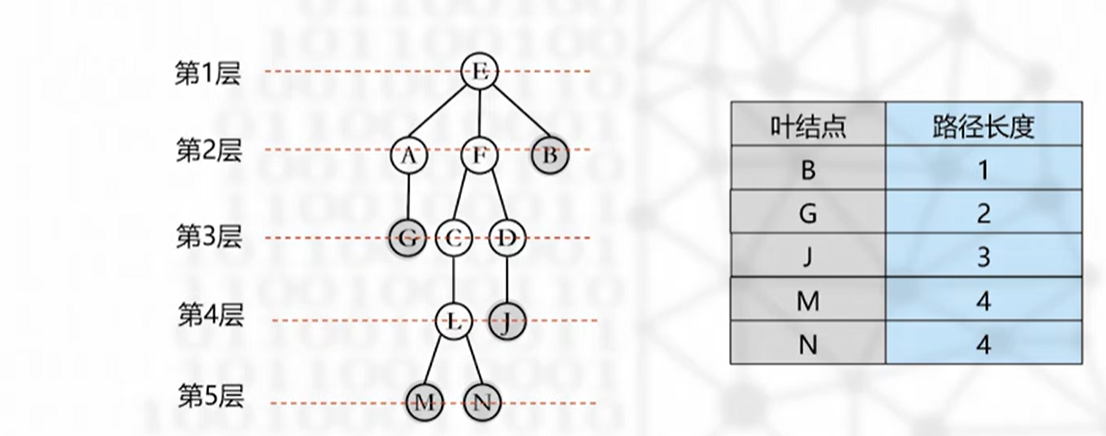
外路径长度=1+2+3+4+4=14
扩充二叉树-补
内路径长度:I
外路径长度:E
非叶节点个数:n
$$
E=I+2n
$$
叶结点的加权路径长度:设叶结点带权——>路径长度×权值
树的加权路径长度(WPL):所有叶结点的加权路径长度
怎么使加权路径长度变大:让权值大的结点远离根结点
哈夫曼算法和哈夫曼树
哈夫曼算法:求具有最小加权路径长度二叉树的算法
哈夫曼树:用哈夫曼算法构造生成的二叉树
- 扩充二叉树
- 任一非叶结点的权值等于其左右孩子的权值之和
- 叶结点相同,哈夫曼树的加权路径长度最小
注:一般树根权值较小的为左子树
哈夫曼编码
压缩编码的原则
- 无二义性——编码,解码均具有唯一性
- 压缩率 与 编/解码效率 的平衡
等长编码和不等长编码
等长编码:元素对应的编码长度相等
不等长编码:元素对应的编码长度不一定相等
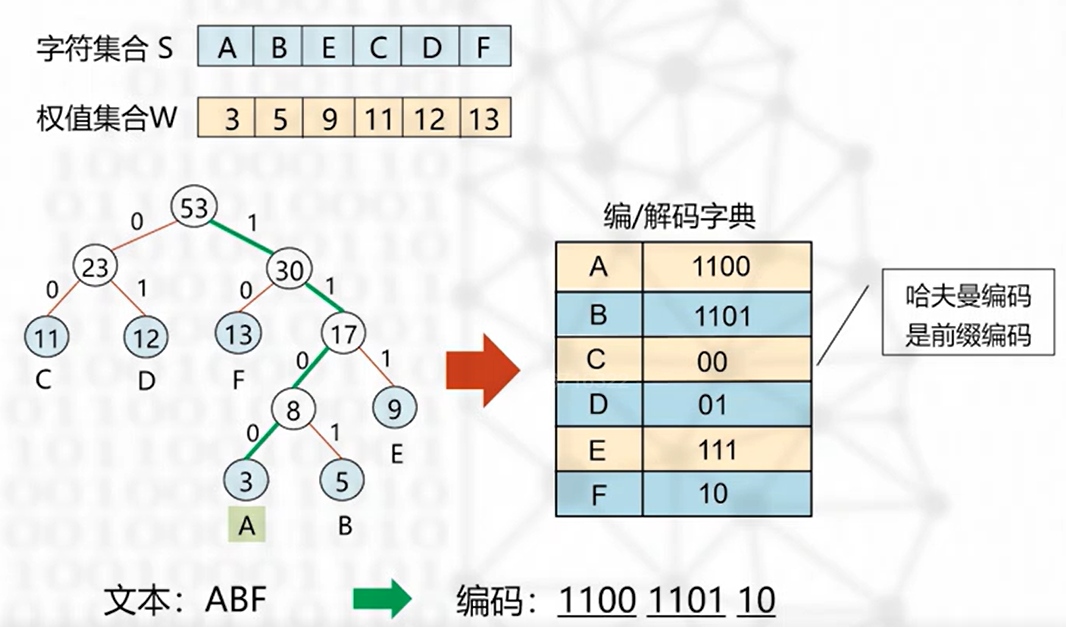
哈夫曼树
http://example.com/2024/11/06/哈夫曼树/