搜索树

二叉搜索树

定义

结点由关键字值表征
假定所有结点关键字值不同
具有如下性质
- 可以是空二叉树
- 若左子树不空，则其上所有结点的关键字值均小于根结点
- 若右子树不空，则其上所有结点的关键字值均大于根结点
- 左右子树也分别为二叉搜索树

性质

中序遍历->关键字值递增

搜索操作

空——>失败
小于——>左子树
大于——>右子树
等于——>结束

插入操作

查找插入元素的位置
1. 从根结点向下搜索
2. 搜索失败的地方作为元素 x 的插入位置
  1. 有重复元素，返回 Duplicate，不进行重复插入！
  2. 搜索到达空子树，则不含重复元素
生成新结点
1. 构造新结点 p 存放新元素 x
插入新结点（可能修改根结点）
1. 新结点在间断处的下一层
2. 左/右取决于关键字大小的比较
3. 原二叉搜索树为空树，则新结点为新树的根

TreeNode *insert(TreeNode *node, int key)
{
    // 如果当前节点为空，创建一个新节点并返回
    if (node == nullptr)
    {
        return new TreeNode(key);
    }

    // 如果待插入的键值小于当前节点的值，
    // 则递归地插入到当前节点的左子树
    if (key < node->val)
    {
        node->left = insert(node->left, key);
    }
    else
    {
        // 否则，递归地插入到当前节点的右子树
        node->right = insert(node->right, key);
    }

    // 返回当前节点指针
    return node;
}

删除操作

删除叶子结点

直接删

删除有一个孩子的结点

先把目标结点的前一个结点和后一个结点相连，再把目标结点释放

删除有两个孩子的结点

在目标结点的后代中选一个替代者覆盖待删除结点，替代者要满足：

能保持二叉搜索树的有序性（待删除结点左子树结点值<=代替者<=待删除结点右子树结点值）
容易删除（1个或没有孩子）
然后删除重复的替代者

代替者的选择方法

中序遍历，目标结点的前一项或后一项

// 获取以 node 为根节点的子树中的最小值节点
TreeNode *getMinValueNode(TreeNode *node)
{
    TreeNode *current = node; // 从传入的节点开始查找
    // 循环查找最左侧的节点，即最小值
    while (current && current->left != nullptr)
    {
        current = current->left; // 移动到左子节点
    }
    return current; // 返回找到的最小值节点
}

// 删除指定键值的节点
TreeNode *deleteNode(TreeNode *node, int key)
{
    // 如果当前节点为空，直接返回
    if (node == nullptr)
    {
        return node;
    }

    // 针对键值进行比较，决定递归地向左子树或右子树查找
    if (key < node->val)
    {
        node->left = deleteNode(node->left, key);
    }
    else if (key > node->val)
    {
        node->right = deleteNode(node->right, key);
    }
    else
    {
        // 找到要删除的节点
        if (node->left == nullptr)
        {
            return node->right; // 如果左子树为空，返回右子树
        }
        else if (node->right == nullptr)
        {
            return node->left; // 如果右子树为空，返回左子树
        }

        // 找到右子树的最小值节点
        TreeNode *minLargerNode = getMinValueNode(node->right);
        node->val = minLargerNode->val;                            // 用最小值节点的值替换当前节点值
        node->right = deleteNode(node->right, minLargerNode->val); // 删除最小值节点
    }
    return node; // 返回当前节点
}

二叉平衡树（AVL树）

定义

二叉平衡树：

根的左右子树高度差的绝对值不超过 1
根的左右子树都是二叉平衡树

结点平衡因子：左子树高度-右子树高度

使用二叉平衡树可以将树的高度稳定在对数级别，这样可以较好的提高搜索等的性能

插入运算

基本原则

先按普通二叉搜索树方法插入，保持排序性
再判断平衡性是否被破坏，决定是否要调整

怎么检查平衡性

从最后一次更新的结点向上回溯，重新判断结点平衡因子，出现平衡因子绝对值大于 1 的情况，即为平衡性被破坏

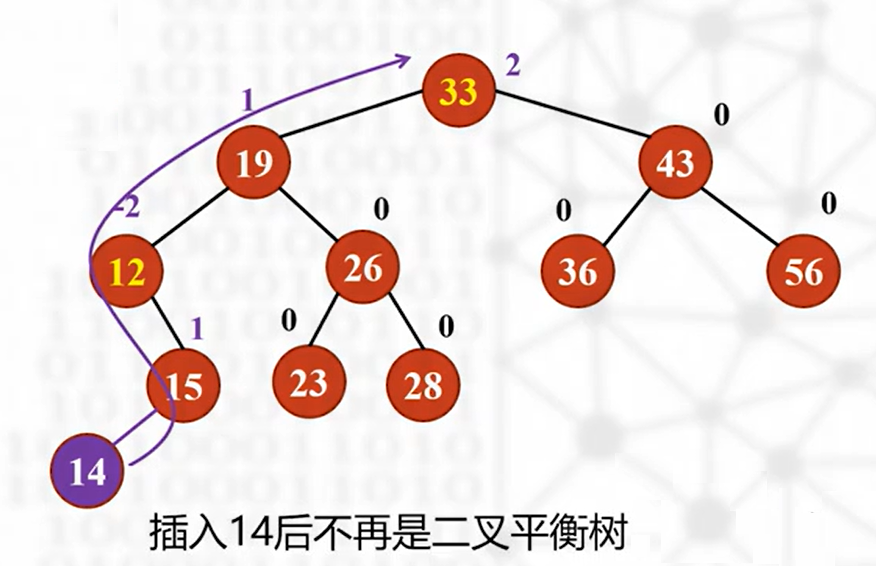
insert_bbt

关键代码：

// 获取平衡因子
int getBalance(AVLTreeNode<T>* node) {
    return node ? getHeight(node->left) - getHeight(node->right) : 0;
}

怎么调整恢复平衡性

找到需要调整的最小子树
调整

最小非平衡结点：离新插入结点最近的非平衡结点

单旋转方法

适用于：LL（RR）插入类型，即新结点插入左子树的左子树，或右子树的右子树——>即直线形式的插入

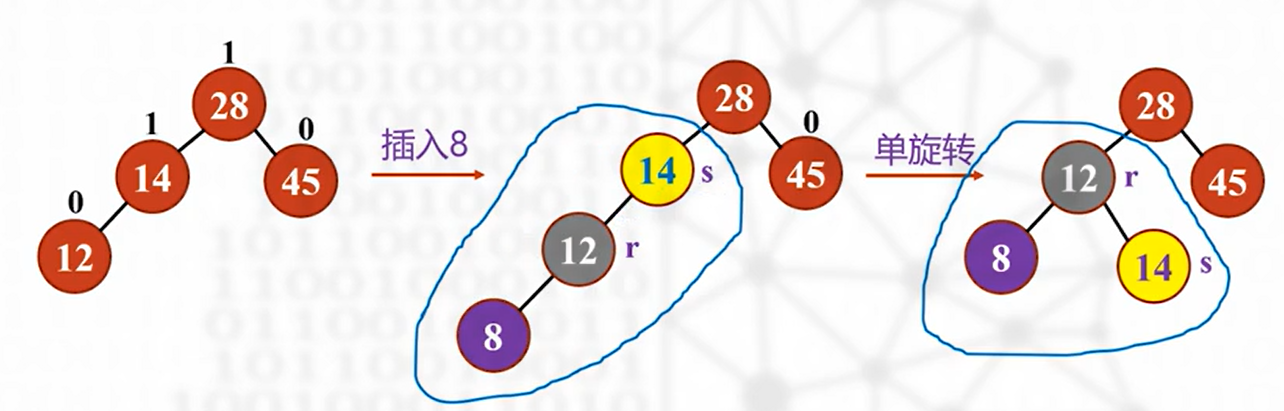
Single_Rotation

双旋转方法

适用于 LR（RL）插入类型——>即折线形式的插入

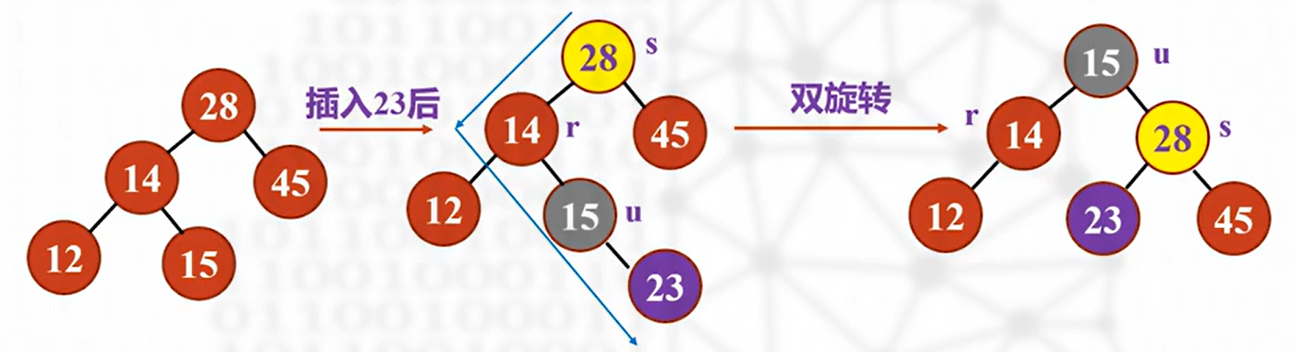
double_1

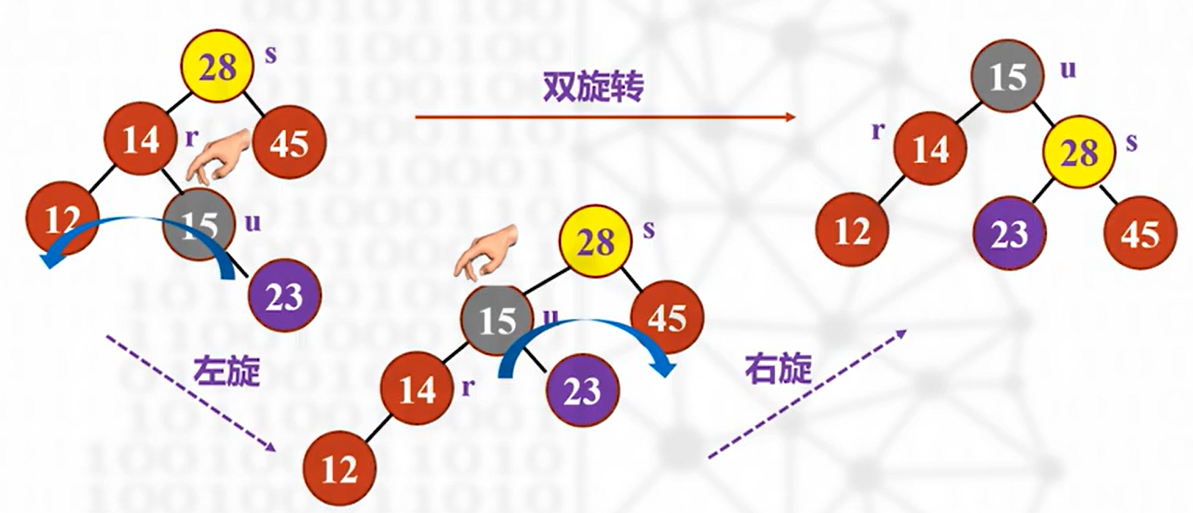
double_2

速通方法

转来转去看懵逼了，想想办法吧

不管是单旋转调整还是双旋转调整：

找到最小非平衡结点
将离根结点最近的3个结点直接构成一个子树进行重排，排完将根结点插回去
新子树除了新根结点的分支需要修改，其它直接保留就行
新根结点的原分支中，只有第一个子节点需要调整，如果它还有后续，不需要改动

B-树

m叉搜索树的定义及性质

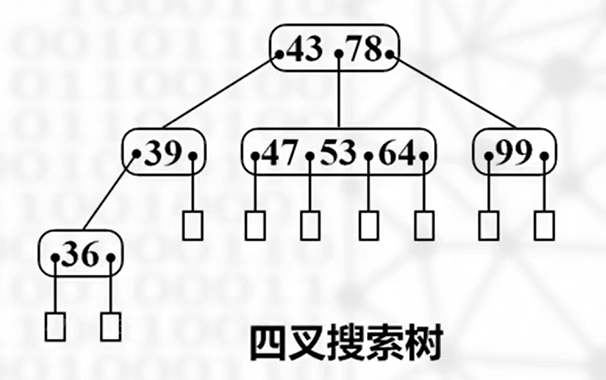
方块：空树（失败结点），不是叶子结点——>搜索某个关键字不在树中时到达的子树

每个结点可以有超过两棵子树
每两棵子树间夹一个关键字
结点中关键字、同一层关键字都是递增的
如果有的话，关键字：左<中<右

一个 m 叉搜索树的结点中，最多存放 m-1 个元素和 m 个指向子树的指针，且每个结点中包含的元素个数总是比包含的指针数少 1

性质

高度为 h 的 m 叉搜索树中最多有 m^h-1 个元素
$$
结点数_{max}=1+m+…+m^{h-1}=\frac{m^h-1}{m-1}
$$
且每个结点最多有 m-1 个元素
含有 N 个元素的 m 叉搜索树高度在 log_m(N+1) 到 N 之间

内搜索和外搜索

内存的存取速度比磁盘快一w~百w，设法减少磁盘存取操作的次数是外搜索算法设计应充分考虑的问题

内搜索：集合足够小，可以在内存中搜索（一般：二叉平衡树）

外搜索：内存不够大，只能放在外存中处理（B-树）

B-树的定义及性质

空树或满足下列特性：

根结点至少有 2 个孩子，根结点可以只含有 1 个元素
除根结点和失败结点外的所有结点至少有 m/2（向上取整）个孩子
所有失败结点在同一层

性质

元素总数 N = 失败结点数 s - 1
含有 N 个元素的 m 阶 B-树的高度 h 有：h<=1+log_m/2(N+1)/2，其中 m/2 向上取整

B-树的插入

搜索

搜索新元素，存在就不插入；若不存在，将新元素插在失败结点的上一层叶子结点中

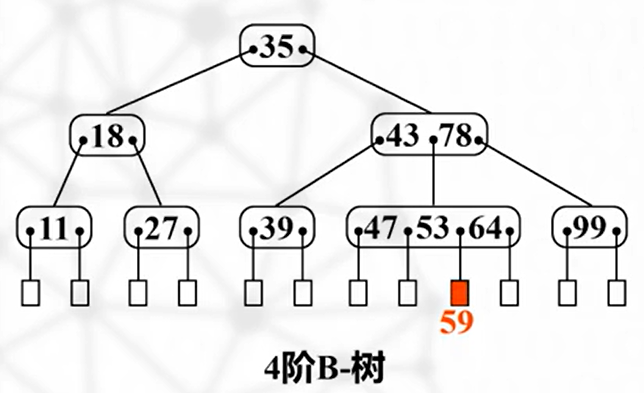
insert_1

插入

将新元素和一个空指针插入

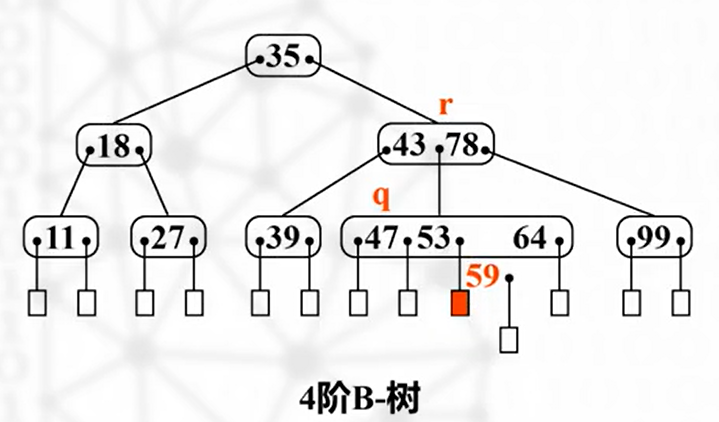
insert_2

检查和分裂

以 m/2（向上取整）处的元素为分割点：该元素前，该元素，该元素后，共3部分

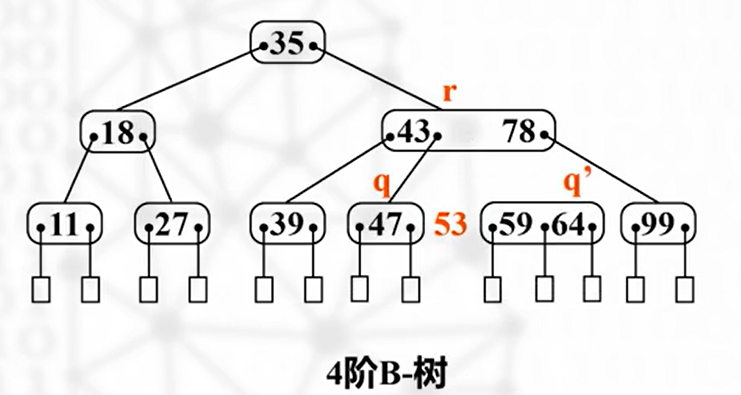
insert_3

前一段和原父结点匹配，将该元素上移成为后一段的父结点

insert_4

检查该元素所在的结点，如果还出现上溢出，重复操作；若根结点产生分裂，将导致 B-树长高一层

B-树的删除

搜索

不存在则失败
存在，判断是否在叶结点上

delete_1

删除

叶结点：直接删除，检查下溢出

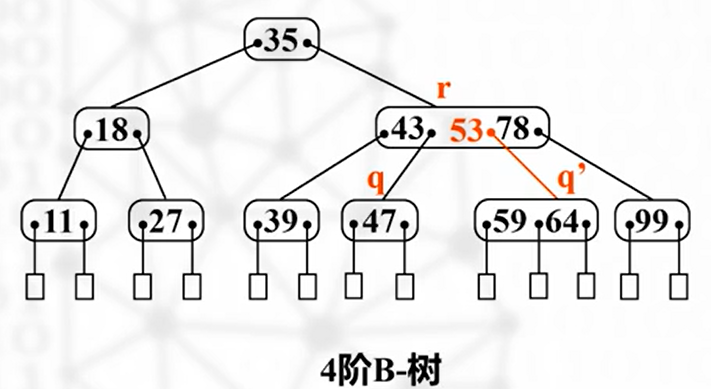
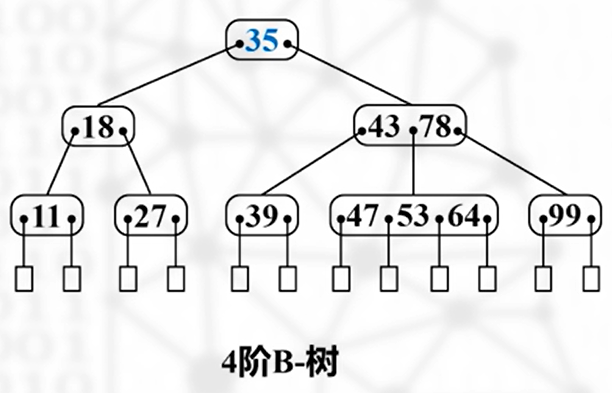
非叶结点：替代操作——右侧子树上的最小元素取代

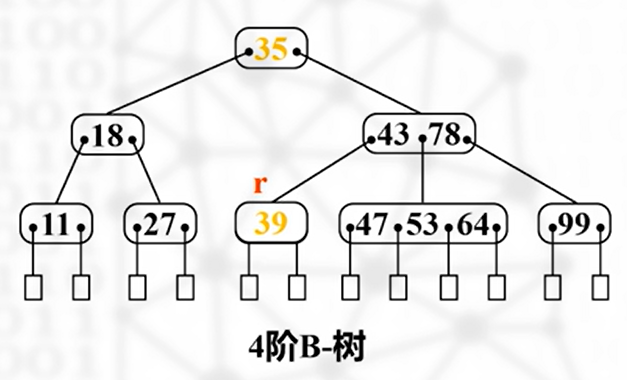
delete_2

然后把该最小元素删除，检查下溢出

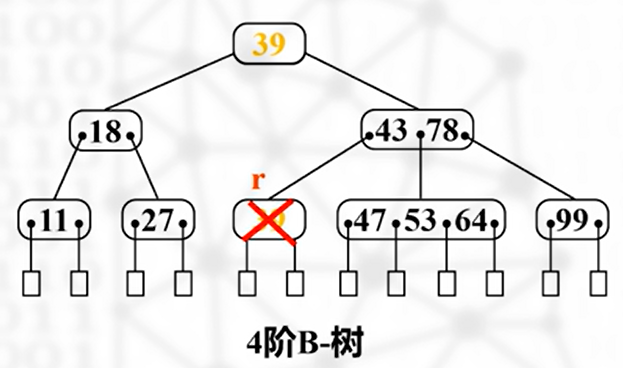
delete_3

下溢出

如下图，r 处出现下溢出，此时需要向同胞兄弟结点借用元素（如果左右两侧兄弟有富余的话）

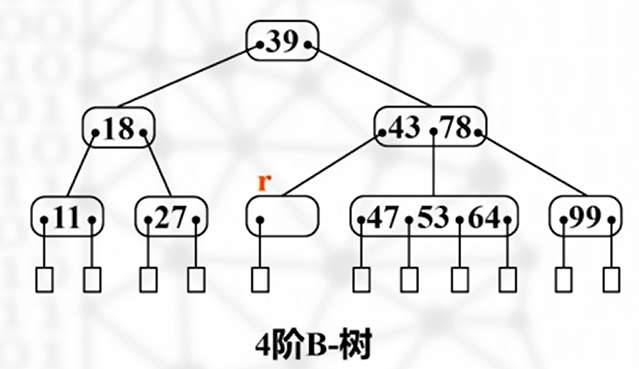
delete_4

借用结点对应的父结点元素

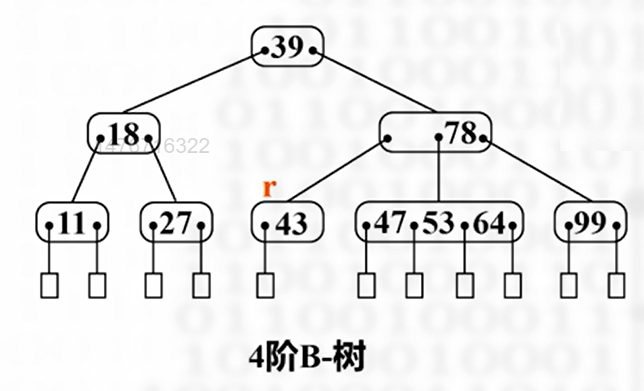
delete_5

父结点缺失的位置向兄弟节点借

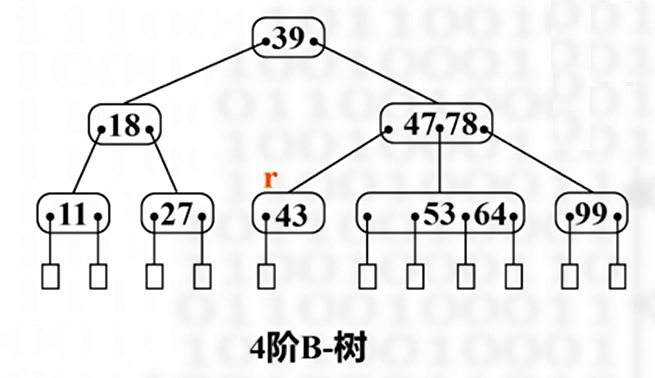
delete_6

将元素和结点一起借走（如果有子树，一起借走）

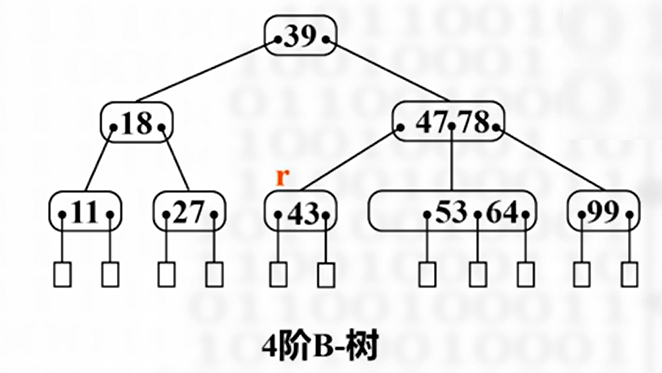
delete_7

若发生下溢出且无富余元素的兄弟，可将下溢出结点与其左/右兄弟合并（优先左），同时将双亲结点中夹在左右侧子树的元素下移到合并后的结点中形成新的结点

如果由于并操作，导致根结点中的一个元素被删除，且该结点只包含一个元素，则根结点变空结点，B-树矮一层

代码示例

代码只需要使用两个库

1 2	`#include <iostream> #include <vector>`

通过模板和类对相关操作进行封装

template<typename T>
class BTreeNode {
public:
    bool isLeaf;                      // 表示是否是叶子节点
    std::vector<T> keys;              // 存储关键字
    std::vector<BTreeNode<T>*> children; // 存储指向孩子节点的指针
    int degree;                       // 每个节点的最小度数

    BTreeNode(int _degree, bool _isLeaf) : degree(_degree), isLeaf(_isLeaf) {}

    void insertNonFull(T key);
    void splitChild(int i, BTreeNode<T>* y);
    void traverse();                  // 添加遍历方法
    void remove(T key);
    void fill(int idx);
    void merge(int idx);
    bool search(T key);
    void borrowFromPrev(int idx);
    void borrowFromNext(int idx);
};

template<typename T>
class BTree {
private:
    BTreeNode<T>* root;               //树的根节点
    int degree;                       //最小度
public:
    BTree(int _degree) : root(nullptr), degree(_degree) {}

    void traverse() {
        if (root) {
            root->traverse();
        }
    }

    void insert(T key);
    void remove(T key);
    
    // 添加搜索方法
    bool search(T key) {
        return root ? root->search(key) : false;
    }
};

在 BTreeNode 中添加多种方法作为成员函数

template<typename T>
bool BTreeNode<T>::search(T key) {
    int idx = 0;
    while (idx < keys.size() && keys[idx] < key) {
        idx++;
    }

    // 如果找到关键字
    if (idx < keys.size() && keys[idx] == key) {
        return true;
    }

    // 如果是叶子节点，则没有找到
    if (isLeaf) {
        return false;
    }

    // 否则递归地在合适的子节点中搜索
    return children[idx]->search(key);
}

template<typename T>
void BTreeNode<T>::insertNonFull(T key) {
    int i = keys.size() - 1;

    if (isLeaf) {
        // 插入到叶子节点
        keys.push_back(key);
        while (i >= 0 && keys[i] > key) {
            keys[i + 1] = keys[i];
            i--;
        }
        keys[i + 1] = key;
    } else {
        // 找到合适的孩子节点插入
        while (i >= 0 && keys[i] > key) {
            i--;
        }
        if (children[i + 1]->keys.size() == 2 * degree - 1) {
            splitChild(i + 1, children[i + 1]);
            if (keys[i + 1] < key) {
                i++;
            }
        }
        children[i + 1]->insertNonFull(key);
    }
}

template<typename T>
void BTreeNode<T>::splitChild(int i, BTreeNode<T>* y) {
    BTreeNode<T>* z = new BTreeNode<T>(y->degree, y->isLeaf);
    z->keys.resize(degree - 1);

    // 将y的后半部分的关键字移动到z
    for (int j = 0; j < degree - 1; j++) {
        z->keys[j] = y->keys[j + degree];
    }

    if (!y->isLeaf) {
        z->children.resize(degree);
        for (int j = 0; j < degree; j++) {
            z->children[j] = y->children[j + degree];
        }
    }

    // 在父节点中插入新子节点的关键字
    keys.insert(keys.begin() + i, y->keys[degree - 1]);
    children.insert(children.begin() + i + 1, z);
    
    y->keys.resize(degree - 1);
}

下面是插入操作

template<typename T>
void BTree<T>::insert(T key) {
    // 检查树是否为空
    if (root == nullptr) {
        // 如果树为空，创建一个新的根节点，并将第一个关键字插入
        root = new BTreeNode<T>(degree, true);
        root->keys.push_back(key);
    } else {
        // 如果根节点已满（即关键字数达到了最大值）
        if (root->keys.size() == 2 * degree - 1) {
            // 创建一个新的非叶子节点以成为新的根节点
            BTreeNode<T>* s = new BTreeNode<T>(degree, false);
            // 将旧根节点作为新根节点的子节点添加
            s->children.push_back(root);
            // 对满的根节点进行分裂，并将中间的关键字上升到新根
            s->splitChild(0, root);
            // 确定要插入的子节点位置
            int i = 0;
            if (s->keys[0] < key) {
                i++; // 根据关键字与新根的第一个关键字进行比较，选择相应的子节点
            }
            // 在合适的子节点中插入关键字
            s->children[i]->insertNonFull(key);
            // 更新根节点为新创建的非叶子节点
            root = s;
        } else {
            // 如果根节点未满，则直接在根节点中插入关键字
            root->insertNonFull(key);
        }
    }
}

然后是删除操作

template<typename T>
void BTreeNode<T>::remove(T key) {
    int idx = 0;
    while (idx < keys.size() && keys[idx] < key) {
        idx++;
    }

    // 找到要删除的关键字
    if (idx < keys.size() && keys[idx] == key) {
        // 找到关键字，在叶子节点中
        if (isLeaf) {
            keys.erase(keys.begin() + idx); // 删除关键字
        } else {
            // 删除非叶子节点的关键字
            // 使用前驱替换
            if (children[idx]->keys.size() >= degree) {
                T pred = children[idx]->keys.back();
                remove(pred); // 删除前驱
                keys[idx] = pred; // 替换为前驱
            }
            // 使用后继替换
            else if (children[idx + 1]->keys.size() >= degree) {
                T succ = children[idx + 1]->keys.front();
                remove(succ); // 删除后继
                keys[idx] = succ; // 替换为后继
            }
            // 合并子节点
            else {
                merge(idx);
                children[idx]->remove(key); // 在合并后的节点中删除
            }
        }
    } else {
        // 如果当前节点是叶子节点，可以直接返回
        if (isLeaf) {
            return;
        }

        // 递归到下一个子节点去删除
        bool shouldMerge = (idx == keys.size());
        if (children[idx]->keys.size() < degree) {
            fill(idx);
        }
        
        // 递归删除
        if (shouldMerge && idx > keys.size()) {
            children[idx - 1]->remove(key);
        } else {
            children[idx]->remove(key);
        }
    }
}

template<typename T>
void BTreeNode<T>::fill(int idx) {
    // 检查当前节点的兄弟节点并借用关键字或合并
    if (idx != 0 && children[idx - 1]->keys.size() >= degree) {
        borrowFromPrev(idx);
    } else if (idx != keys.size() && children[idx + 1]->keys.size() >= degree) {
        borrowFromNext(idx);
    } else {
        // 合并
        if (idx != keys.size()) {
            merge(idx);
        } else {
            merge(idx - 1);
        }
    }
}

template<typename T>
void BTreeNode<T>::borrowFromPrev(int idx) {
    // 从前一个兄弟节点借一个关键字
    BTreeNode<T>* child = children[idx];
    BTreeNode<T>* sibling = children[idx - 1];

    // 移动所有关键字到右
    child->keys.insert(child->keys.begin(), keys[idx - 1]);
    keys[idx - 1] = sibling->keys.back();
    sibling->keys.pop_back();

    // 移动子节点
    if (!child->isLeaf) {
        child->children.insert(child->children.begin(), sibling->children.back());
        sibling->children.pop_back();
    }
}

template<typename T>
void BTreeNode<T>::borrowFromNext(int idx) {
    // 从下一个兄弟节点借一个关键字
    BTreeNode<T>* child = children[idx];
    BTreeNode<T>* sibling = children[idx + 1];

    // 将分隔关键字放入子节点
    child->keys.push_back(keys[idx]);
    keys[idx] = sibling->keys.front();
    sibling->keys.erase(sibling->keys.begin());

    // 移动子节点
    if (!child->isLeaf) {
        child->children.push_back(sibling->children.front());
        sibling->children.erase(sibling->children.begin());
    }
}

template<typename T>
void BTreeNode<T>::merge(int idx) {
    // 将一个子节点与其兄弟节点合并
    BTreeNode<T>* child = children[idx];
    BTreeNode<T>* sibling = children[idx + 1];

    // 将分隔关键字移到子节点中
    child->keys.push_back(keys[idx]);
    child->keys.insert(child->keys.end(), sibling->keys.begin(), sibling->keys.end());

    // 复制子节点
    if (!child->isLeaf) {
        child->children.insert(child->children.end(), sibling->children.begin(), sibling->children.end());
    }

    // 移动关键字
    keys.erase(keys.begin() + idx);
    children.erase(children.begin() + idx + 1);
}

template<typename T>
void BTree<T>::remove(T key) {
    if (!root) {
        std::cout << "树为空，无法删除\n";
        return;
    }

    // 在删除之前先检查关键字是否存在
    if (!search(key)) {
        std::cout << "关键字 " << key << " 不存在，无法删除\n";
        return;
    }

    root->remove(key);

    // 如果根节点变为空，更新根节点
    if (root->keys.empty()) {
        BTreeNode<T>* oldRoot = root;
        if (root->isLeaf) {
            root = nullptr; // 树变为空
        } else {
            root = root->children[0]; // 更新根为第一个子节点
        }
        delete oldRoot; // 释放内存
    }
}

输出操作

template<typename T>
void BTreeNode<T>::traverse() {
    int i;
    // 遍历当前节点的所有关键字
    for (i = 0; i < keys.size(); i++) {
        // 如果当前节点不是叶子节点
        if (!isLeaf) {
            // 递归遍历当前节点的第 i 个子节点
            children[i]->traverse();
        }
        // 输出当前节点的第 i 个关键字
        std::cout << keys[i] << " ";
    }
    // 如果当前节点不是叶子节点，则遍历最后一个子节点
    if (!isLeaf) {
        children[i]->traverse();
    }
}

通过主函数进行调用

int main() {
    BTree<int> bTree(3); // 创建一个最小度为3的B-树

    bTree.remove(4);

    bTree.insert(10);
    bTree.insert(20);
    bTree.insert(5);

    bTree.remove(4);
    
    bTree.insert(6);
    bTree.insert(12);
    bTree.insert(30);
    bTree.insert(7);
    bTree.insert(17);

    std::cout << "B-树的遍历结果为: ";
    bTree.traverse();
    std::cout << std::endl;

    bTree.remove(10);
    std::cout << "B-树的删除10后的遍历结果为: ";
    bTree.traverse();
    std::cout << std::endl;

    return 0;
}s

输出结果

树为空，无法删除
关键字 4 不存在，无法删除
B-树的遍历结果为: 5 6 7 10 12 17 20 30 
B-树的删除10后的遍历结果为: 5 6 7 12 17 20 30

数据结构

#数据结构

搜索树

http://example.com/2024/11/17/搜索树/

作者

Tsglz

发布于

2024年11月17日

许可协议

散列表上一篇

集合和搜索下一篇