图

图的基本结构

G=(V，E)，其中 V 代表 G 中结点的有限非空集合，E 为 G 中边的有限集合

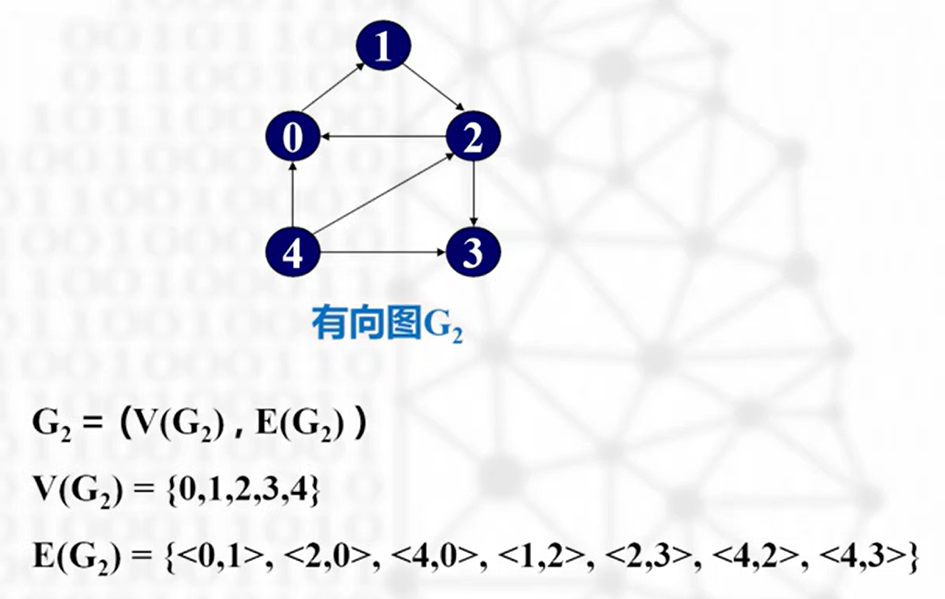
有序（有向图）

用 <u,v> 表示一条有向边

注：u 为始点（尾），v 为终点（头）

flowchart LR
	u-->v

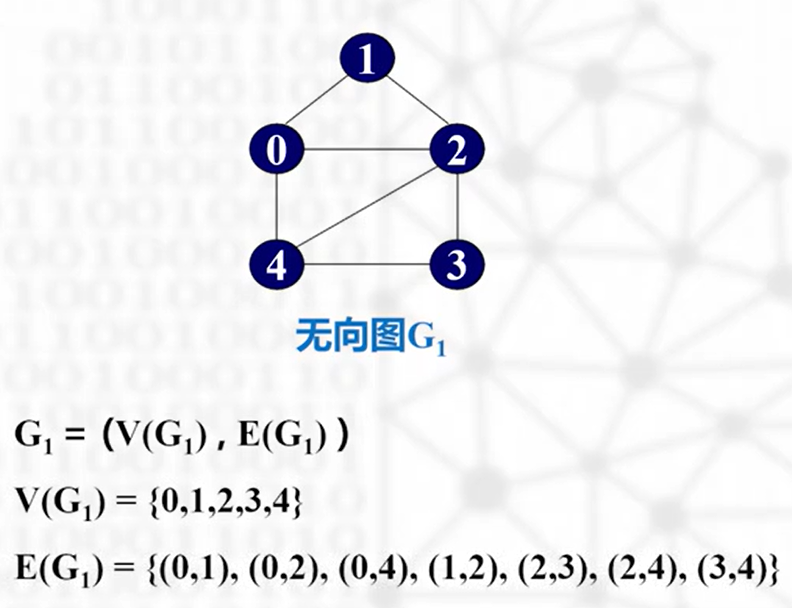
无序（无向图）

（u，v）和（v，u）是同一条边

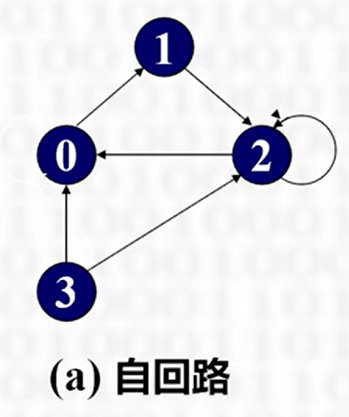
自回路

存在无向边（u，u）或有向边 <u，u>

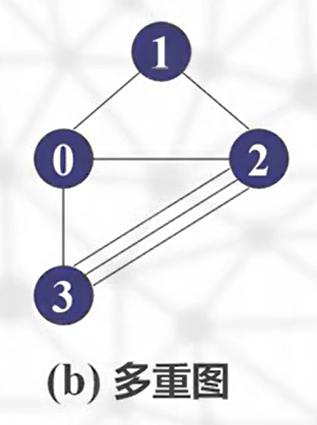
多重图

两个顶点间允许有多条相同边

完全图

有最多的边数

• n个顶点
  • 无向完全图：n(n-1)/2 条边
  • 有向完全图：n(n-1) 条边

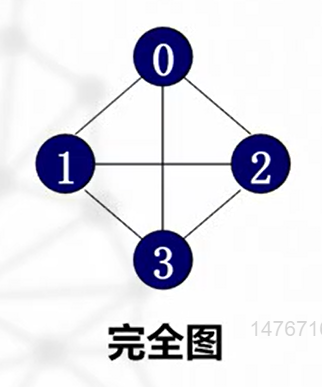
邻接：有边连接的两个顶点
关联：边和顶点连接的关系

连通图

连通：两点间存在路径
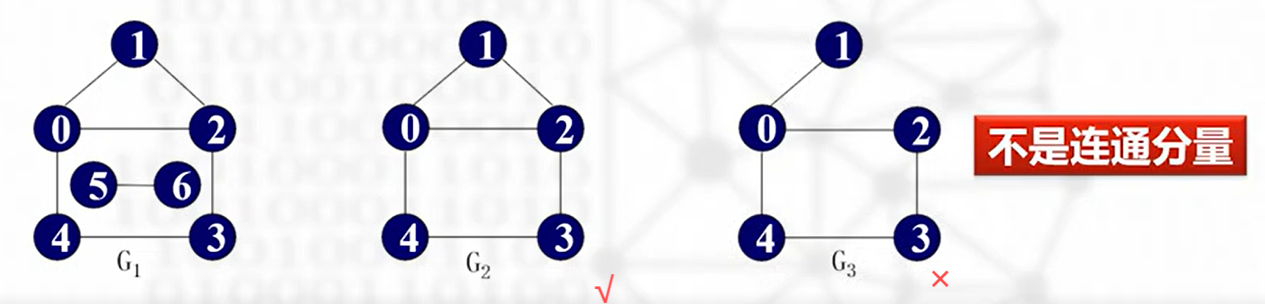
连通图：无向图中任意两个顶点间连通，如下图

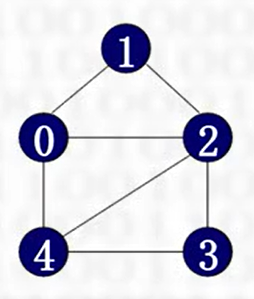
连通分量：无向图的极大连通子图

如下图，为非连通图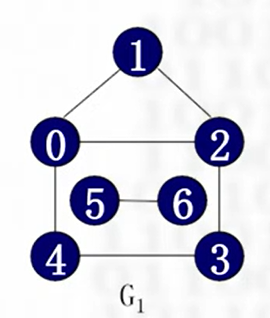

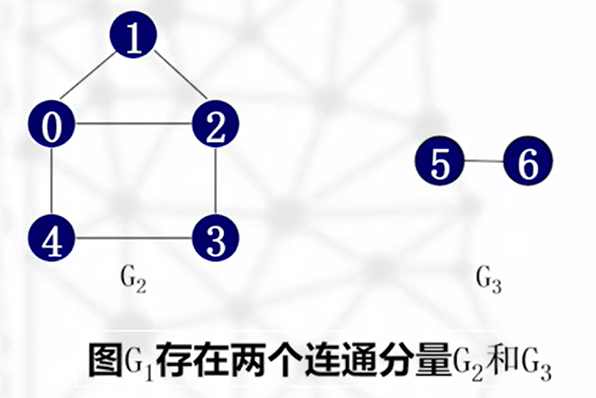
• 连通分量可能有多个，不能只写最大的
• 每个连通分量必须是极大的
• 每个连通分量必须包含其顶点之间的所有边（见下）

强连通图：存在 u 到 v 路径的同时，还存在 v 到 u的路径
强连通分量：有向图的极大强连通子图

度

顶点的度：与该顶点相关联的边的数量
入度：顶点的入度即以该点为头（箭头）的边的数目，出度则为尾

生成树

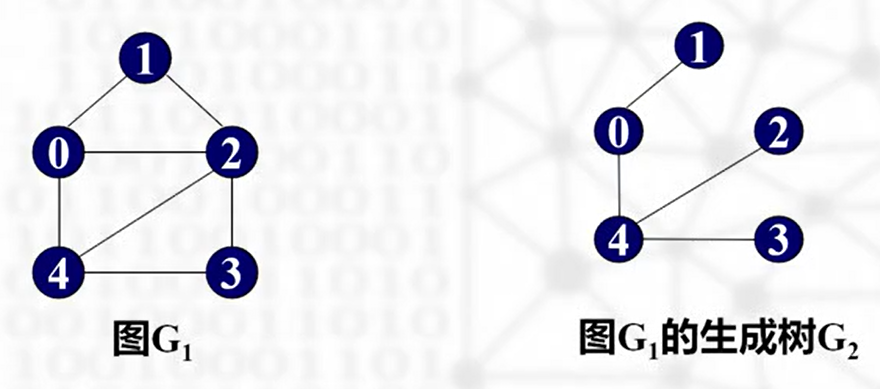
无向连通图的生成树是一个极小连通子图

• 包含所有顶点
• 只有足以构成一棵树的边（n-1），加上一条边将构成回路

网

在图的边上加上数字作为权值（代价）

带权有向图的抽象数据类型

ADT Graph{
数据：
	顶点的有限非空集合V和边集合E，每条边由E中偶对<u，い>表示。
	数据元素之间的关系是多对多的关系。
运算：
	Init（G，n）：初始化运算。构造一个包含n个顶点没有边的图G。
	Destroy（G）：撤销运算。撤销一个图G。
	Exist（G，u，v）：边的搜索运算。若图G中存在边<u，v>，则函数返回OK，否则返回                           Error。
	Insert（G，u，v，w）：边的插入运算。向图G中添加权为w的边<u，v>，若插入成功，返回                          OK；若图中已存在边<u,v>,则返回Duplicate;否则返回Error。
	Remove(G,u,v):边的删除运算。从图G中删除边<u,v>,若图中不存在边<u,v>,则返回                         NotPresent;若图中存在边<u，v>，则从图中删除此边，返回OK；其他返回                   Error。
}

图的存储结构

因过于复杂，没有顺序结构

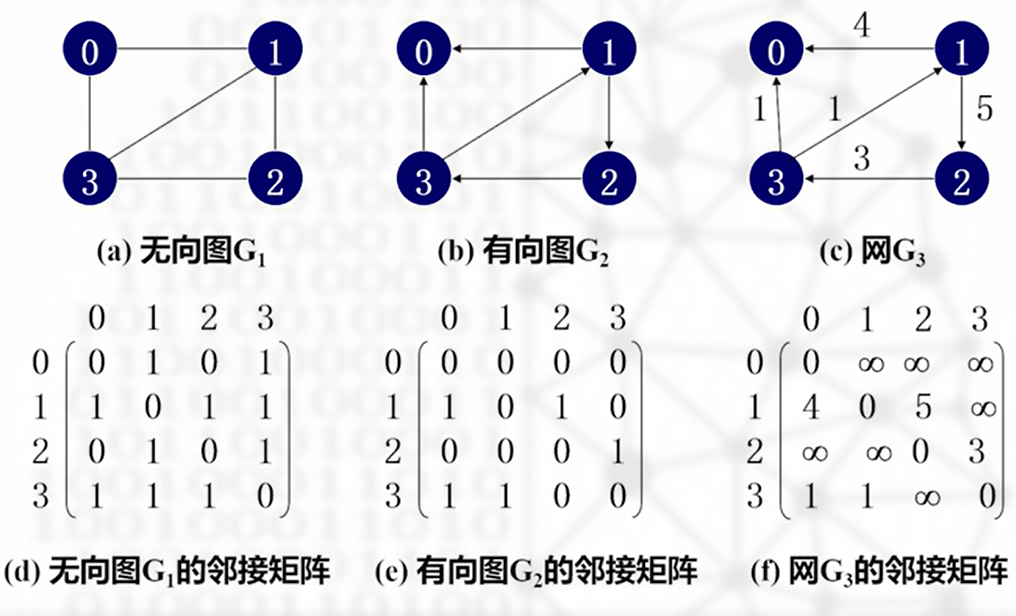
邻接矩阵表示法

邻接矩阵：表示顶点间相邻关系的矩阵

$$
A[u][v] = \begin{cases} 1, & \text{若 } (u,v) \text{ 或 } \langle u,v \rangle \in E \ 0, & \text{否则} \end{cases}
$$

若为网，则可定义为

$$
A[u][v] = \begin{cases} w, & \text{若 } (u,v) \text{ 或 } \langle u,v \rangle \in E \ 0, & \text{若 u=v}
\ \infty, & \text{否则}
\end{cases}
$$
其中，w 表示边上权值，无穷大表示计算机允许的、大于所有边上权值的数

优点

1. 便于判断两个顶点之间是否有边（A[u][v]值）
2. 便于计算各个顶点的度
   1. 无向图：邻接矩阵第 i 行元素和即为顶点 i 的度
   2. 有向图：第 i 行元素和即顶点 i 出度；第 i 列元素和即顶点 i 入度

缺点

• 不便于统计边的数目
  • 时间复杂度为 O(n²)
• 空间复杂度高
  • 空间复杂度为 O(n²)

邻接表表示法

下图为不带权的邻接表示例（未列出保存顶点信息的数据域——应在头尾中间）：

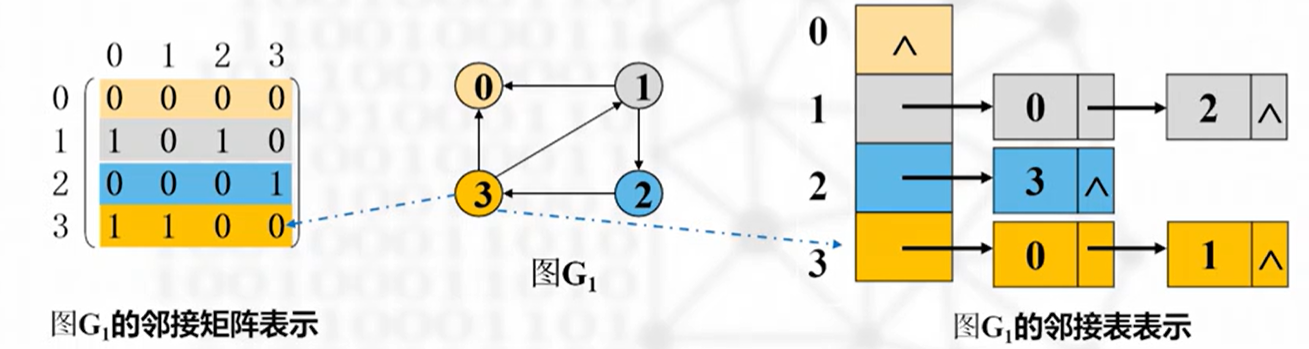
下图分别为带权和不带权的图示（简化条件下的表示可以将头链表转为使用数组代替）

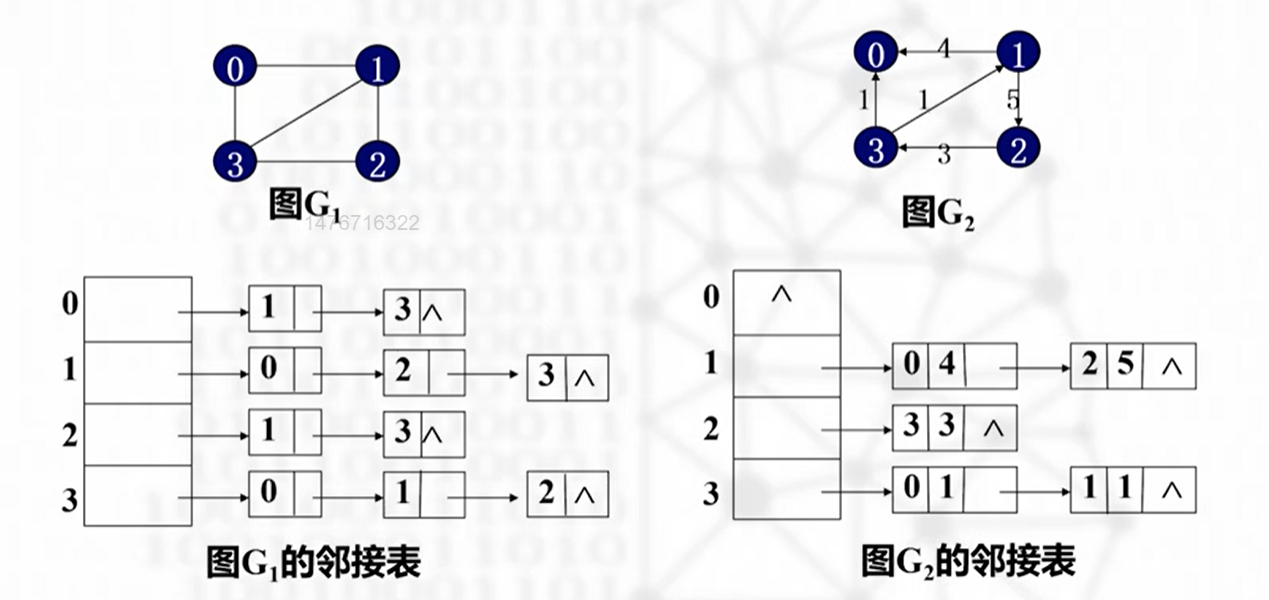
优点

• 便于统计边的数目
  • 时间复杂度 O(n+e)，其中 n 为顶点，e 为边
• 空间效率高
  • 有向图/无向图：O(n+e)
  • 适合稀疏图，稠密图建议邻接矩阵表示法

缺点

• 不便于判断顶点之间是否有边
  • 最坏情况：O(n) 的时间
• 不便于计算有向图各个顶点的度
  • 出度：第 u 个边链表中边结点个数
  • 入读：遍历所有顶点的边链表

图的遍历

图遍历与树遍历的区别

• 可能存在到达不了的顶点
• 可能多次经过同一个顶点（回路）

解决办法：

• 辅助数组（判断是否被访问过）
  • 防止多次访问
  • 搜索结束后如果存在未标记顶点，应从图中另选一个未标记顶点出发，再次搜索

深度优先搜索遍历（DFS）

类似于树的先序遍历，递归

步骤

1. 初始化标记数组
2. 逐个检查顶点，使用 DFS 遍历，直到顶点全部访问完

DFS 操作方法

• 前进
  • 从顶点 v 出发，访问任一未被访问的邻接顶点 w₁
  • 再从 w₁ 出发，重复上述步骤，直到全部访问完
• 回退
  • 回退一步，若存在未被访问邻接顶点，则开始前进，否则继续回退直到遍历完成

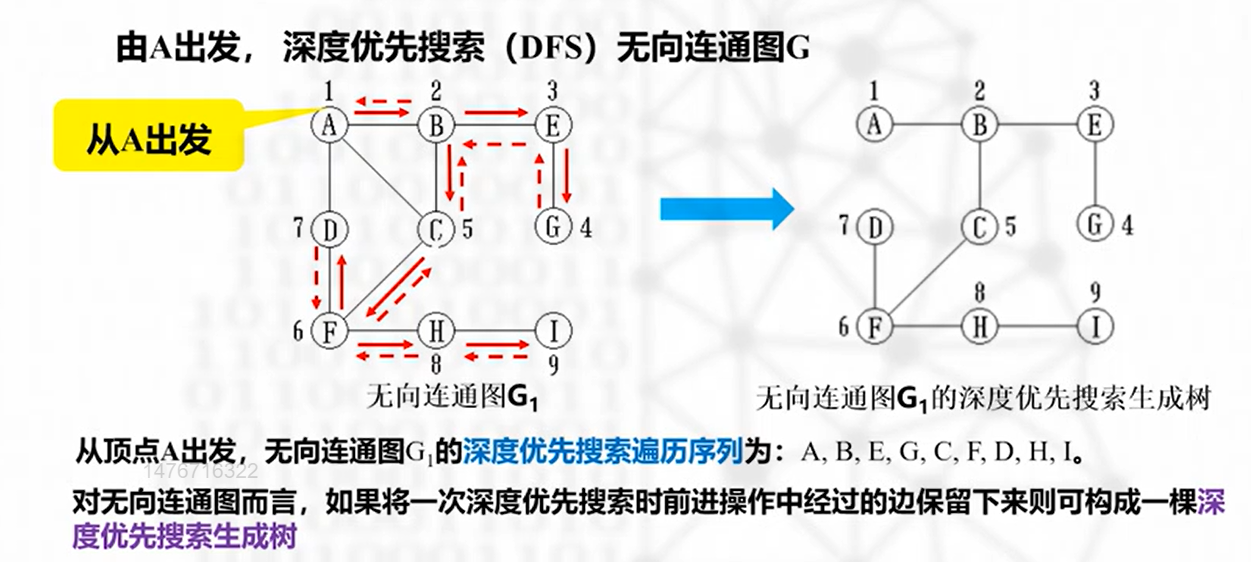
注：如果中间出现路径不连通而导致的重新搜索，会得到 深度优先搜索生成森林

代码示例

void DFS(int v, int visited, LGraph g)
{
	ENode *w;
	printf("%d",v); //访问顶点v
	visited[v]=1;  //为顶点v打上访问标记
	for(w=g.a[v]; w; w=w->nextArc)
	{
		if(!visited[w->adjVex)
			DFS(w->adjVex,visited, g);
	}
}

void DFSTraverse(LGraph g)
{
	int i;
	
	//动态生成标记数组
	int *visited =(int*)malloc(g.n*sizeof(int);
	
	//初始化标记数组
	for(i=0; i<g.n; i++) 
		visited[i]=0;
	
	//逐一检查每个顶点，若未被访问，则调用DFS
	for(i=0; i<g.n; i++)
		if (！visited[i])
			DFS(i, visited, g);
	free(visited);
}

分析

• DFS 对有向图每条边只查看一次，对无向图要 2 次（无向图的边在逻辑上被视为双向）
• 时间复杂度
  • 邻接表存储：O(n+e)，其中 n 为顶点，e 为边
  • 邻接矩阵存储：O(n²)

使用 DFS 查找割点和桥

from collections import defaultdict

def find_articulation_points_and_bridges(graph, n):
    """
    使用 DFS 查找图中的割点和桥。

    :param graph: 邻接表形式表示的图 (defaultdict of lists)
    :param n: 图中节点数
    :return: 割点和桥的列表
    """
    discovery = [-1] * n  # 记录每个节点的发现时间
    low = [-1] * n  # 记录每个节点的低值
    parent = [-1] * n  # 记录每个节点的父节点
    visited = [False] * n  # 记录节点是否被访问

    articulation_points = set()  # 存储割点
    bridges = []  # 存储桥

    time = [0]  # 用于全局时间递增

    def dfs(u):
        visited[u] = True
        discovery[u] = low[u] = time[0]  # 初始化发现时间和低值
        time[0] += 1

        children = 0  # 子节点数量

        for v in graph[u]:
            if not visited[v]:
                parent[v] = u
                children += 1

                dfs(v)

                # 更新当前节点的低值
                low[u] = min(low[u], low[v])

                # 判断割点
                if parent[u] == -1 and children > 1:  # 根节点的特殊情况
                    articulation_points.add(u)
                if parent[u] != -1 and low[v] >= discovery[u]:
                    articulation_points.add(u)

                # 判断桥
                if low[v] > discovery[u]:
                    bridges.append((u, v))

            elif v != parent[u]:  # 更新低值
                low[u] = min(low[u], discovery[v])

    # 遍历所有未访问的节点
    for i in range(n):
        if not visited[i]:
            dfs(i)

    return articulation_points, bridges


# 示例图（邻接表表示）
graph = defaultdict(list)

# 添加边（无向图）
# 示例图来自用户提供的图像，边可能需要根据具体图像调整
edges = [(0, 1), (0, 2), (1, 4), (1, 3), (2, 3), (2, 4), (2, 5), (3, 4), (3, 5)]

for u, v in edges:
    graph[u].append(v)
    graph[v].append(u)

n = 6  # 图中的节点数量

# 查找割点和桥
articulation_points, bridges = find_articulation_points_and_bridges(graph, n)

print("割点:", articulation_points)
print("桥:", bridges)

# 输出最小需要移除的节点或边
if articulation_points:
    print(
        f"至少需要移除 {len(articulation_points)} 个割点或 {len(bridges)} 条桥使图变为非连通。"
    )
else:
    print("图中无割点或桥，无需移除节点或边。")

在上述代码中，只需要画出图像，输入结点，就能很轻松的知道如何将图变为非连通

宽度优先搜索遍历

类似于树的层次遍历，非递归，也没有 DFS 的回退情况

步骤

• 初始化标记数组
• 检查每个顶点，若未被访问，则使用 BFS 遍历

BFS 操作方法

• 从某个顶点出发
• 依次访问未访问过的邻接点，直到都访问完
  • 可以使用队列来保存已访问过但其邻接点尚未考察的顶点

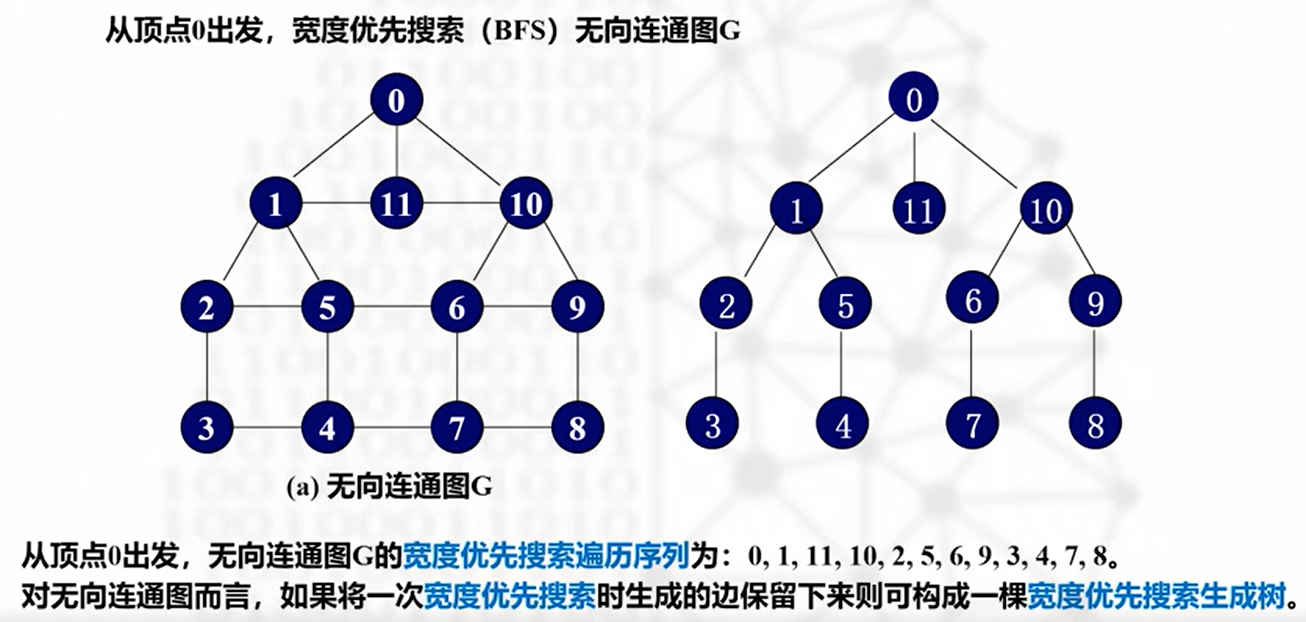
代码示例

void BFS(int v, int visited[l, LGraph g)
{
	ENode *w;
	Queue q;
	
	create(&q,g.n);  //初始化队列
	visited[v]=1；//为顶点v打上访问标记
	printf("%d "，v); //访问顶点v
	EnQueue(&q,v); //将顶点v放入队列
	while (!IsEmpty(&q))
	{
		Front(&q,&u);
		DeQueue(&q); //队首顶点u出队
		for(w=g.a[u];w;w=w->nextArc)
		//依序搜素u的未被访问过的邻接点，访问并将其入队
			if (!visited[w->adjVex])
			{
				visited[w->adjVex]=1;
				printf("%d",w->adjVex);
				EnQueue(&q,w->adjVex);
			}
}

void BFSTraverse(LGraph g)
{
	int i;
	//动态生成访问标记数组
	int *visited =(int*)malloc(g.n*sizeof(int);
	for（i=0；i<g.n；i++）//初始化访问标记数组
		visited[i]=0;
	for（i=0；i<g.n；i++）//依序检查每个顶点，若未被访问，则调用BFS算法以该点为起始点遍历该图
		if (!visited[i])
			BFS(i, visited, g);
	free(visited);
}

分析

• 每个顶点进出队列各一次
• 每个出队顶点，检查所有邻接点，无向图每条边查两次
• 时间复杂度
  • 邻接表存储：O(n+e)，其中 n 为顶点，e 为边
  • 邻接矩阵存储：O(n²)

拓扑排序

顶点活动网络（AOV 网）

顶点代表活动，有向边表示活动之间领先关系的有向图

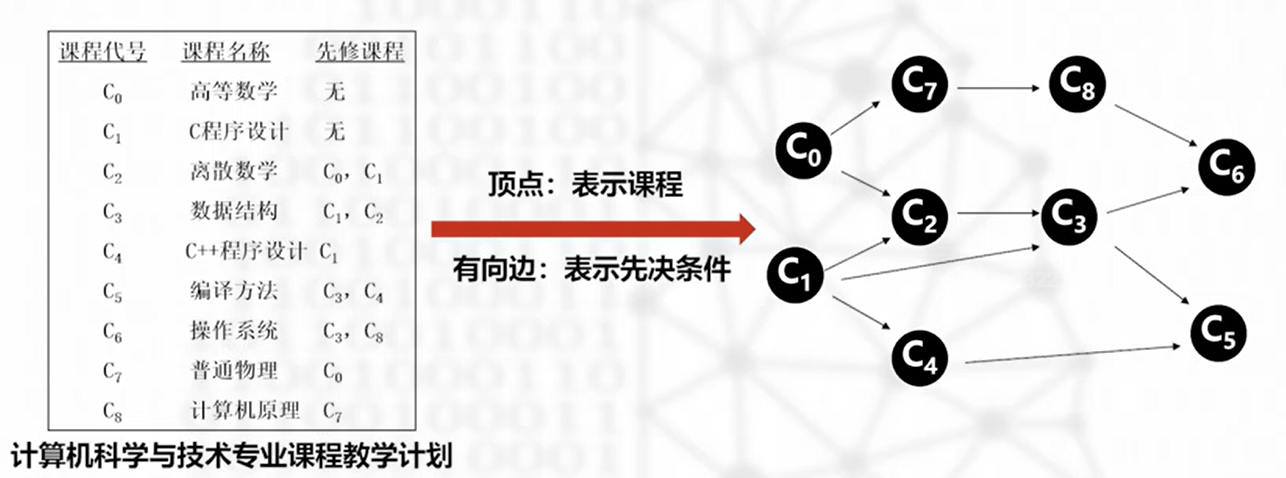
注：AOV 网不应有环，应该是一个有向无环图（DAG 图）

判断 AOV 网是否有环：对有向图顶点进行拓扑排序，若所有顶点都在拓扑序列中，则该 AOV 网必定不存在环

拓扑排序与拓扑序列

拓扑排序

将 AOV 网中所有顶点线性排列

特点：若顶点 a 到 b 有一条路径，则序列中 a 必在 b 之前

拓扑序列

AOV 网中顶点的线性序列

若在网中，a 领先于 b，则在线性序列中 a 是 b 的前驱结点

算法及其实现

拓扑排序过程

1. 找一个入度为 0 的顶点输出
2. 删除该顶点及其所有出边
3. 重复，直到所有顶点都输出（或无入度为 0 的顶点）

基本操作

1. 计算每个顶点的入度
   • 可以计算每个顶点的直接前驱的个数
2. 删除该顶点的所有出边
   • 将该顶点的邻接点入度减一

• 计算各顶点入度存于数组，将入度为 0 的顶点进栈
• 若栈不空，重复
  • 顶点 a 出栈并保存在拓扑序列数组中
  • 将 a 所有邻接点入度减一，若出现减后入度为 0，进栈
• 若还有顶点未输出，表明有环，无法拓扑排序，否则成功

分析

• n 顶点，e 边
  • 计算入度并存于数组：O(e)
  • 初始化堆栈 & 进栈：O(n)
  • 排序过程（有向无环）：顶点各进出一次，入度减一循环 e 次，总计 O(n+e)

关键路径

AOE 网

带权的有向无环图，边权表示活动持续时间。可以用来估算一项工程的完成时间

特点

• 无环情况下，只有一个入度为 0 的点（源点），表示工程开始
• （无环）只有一个出度为 0 的点（汇点），表示工程结束

关键路径

从开始顶点到完成顶点的最长路径

最短时间：关键路径的长度，关键路径上边代表的活动称为关键活动

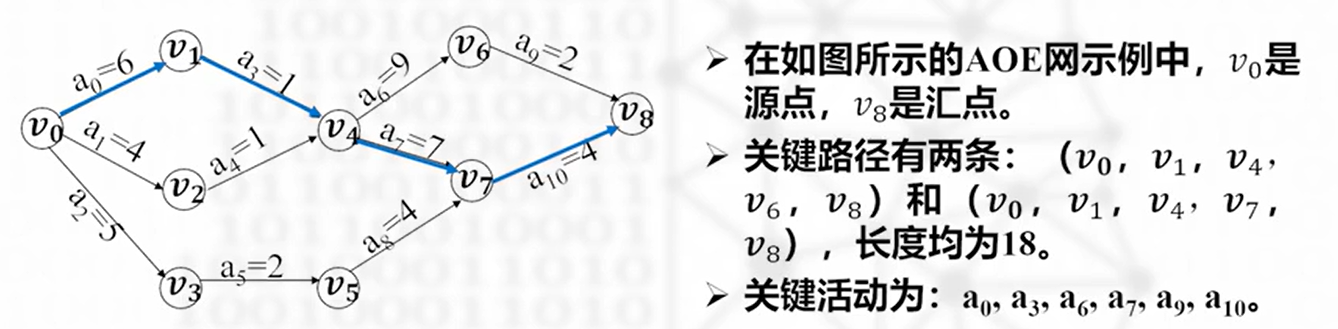
事件相关

事件 a 可能的最早发生时间 E_early(v_i)：开始顶点 v₀ 到 顶点 a 的最长路径长度

事件 a 允许的最迟发生时间 E_late(v_i)：不影响工期的条件下，a 允许的最晚发生时间

活动相关

活动 a 可能的最早开始时间 A_early(a) = E_early(v_i)

活动 a 允许的最迟发生时间 A_late(a) = E_late(v_j)-w(v_i-v_j)（权值）：不影响工期的条件下，a 允许的最晚发生时间

求解关键路径

求解过程~O(n+e)

• 对顶点拓扑排序
• 按拓扑序列求每个事件可能的 E_early(v_i)
• 按逆拓扑序列求每个事件允许的 E_late(v_i)
• 求出每个活动的 A_early(a) 和 A_late(a)
  • 关键活动：A_early(a) = A_late(a)

把它们连起来就是关键路径

最小代价生成树

生成树的代价：各边上的代价之和

最小代价生成树：带权图的各生成树中，具有最小代价的生成树

普里姆算法

过程

• 初始状态：构造生成树 T 只有一个任意选定的起始项点，无边
• 重复执行下列运算：
  • 从 T 的所有入边中找一条代价最小的边 e
  • 将边 e 及其不属于 T 的那个顶点加入 T，直到所有顶点均加入 T 为止
    最小代价生成树 T（包含 n-1 条边）
    注：选择代价最小的入边时，如果存在多条同样权值的边可选，任选其一即可

数据结构

• 邻接表存储
• 3个一维数组
  • 存放与顶点 i 距离最近且在生成树上的顶点
  • 存放边的权值
  • 标记顶点是否已经在生成树上

时间复杂度

n 个顶点，e 条边，O(n²)

克鲁斯卡尔算法

过程

• 初始状态：T 只包含 G 中所有顶点，无边
• 重复：
  • 在 E 中选择一条代价最小的边 (u,v)，并将其从 E 中删除
  • 在生成树边集合中加入 (u,v)，未形成回路，则加入，否则选下一条边
  • 重复直到边集合包含 n-1 条边为止
    最小代价生成树 T（包含 n-1 条边）

数据结构

• 邻接表存储
• 2个一维数组
  • 用于存储图中所有边的信息
    • 两个顶点信息和权值（排序算法选代价最小）
  • 各顶点所属的连通分量（两个顶点属于不同连通分量，则加入它们关联的边后不会形成回路）

时间复杂度

n 个顶点，e 条边，无向图

• 堆排序权值：O(e*log₂e)
• 选择代价最小边加入生成树：O(e*log₂e)

总体时间复杂度：O(e*log₂e)

单源最短路径

最短路径：路径长度最短（路径上边的权值之和最小）

单源最短路径问题：（带权有向图 G 和源点 v₀），求 v₀ 到 V 中其余各顶点的最短路径

Djikstra 算法

按路径长度的非递减次序逐一产生最短路径

求解过程

• 将 V 中顶点分成两组
  • S：已求得最短路径的顶点集合（初始只包括源点）
  • T=V-S：尚未确定最短路径的顶点集合（初始为V-{v₀}）
• 将 T 中顶点按最短路径非递减次序加入 S
  • 计算 v₀ 到 T 中各顶点 v_i 的当前最短路径，取最短为下一条路径，将终点加入 S，直到 S == V

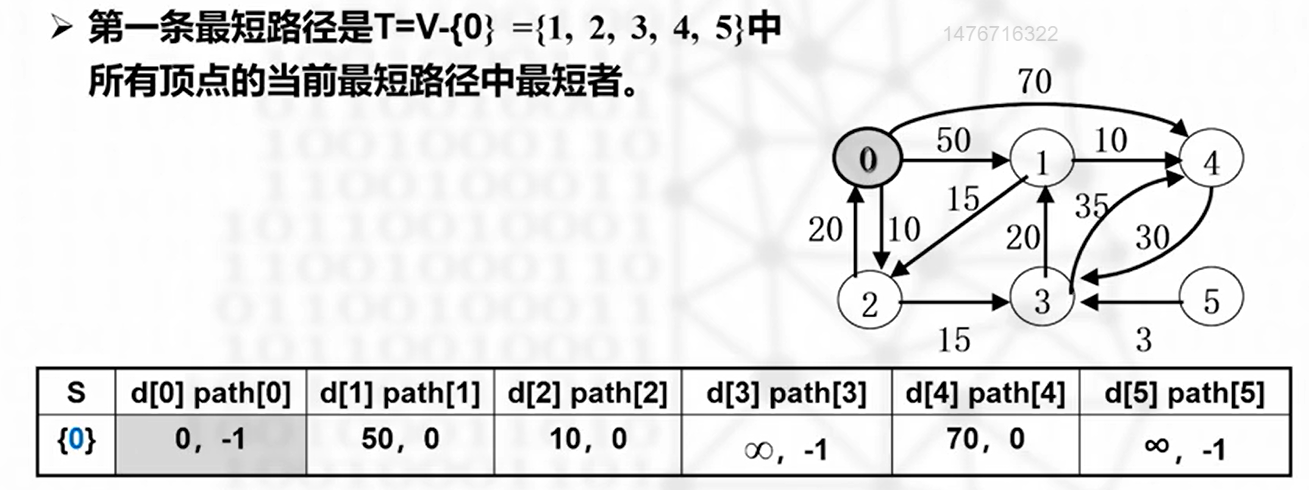
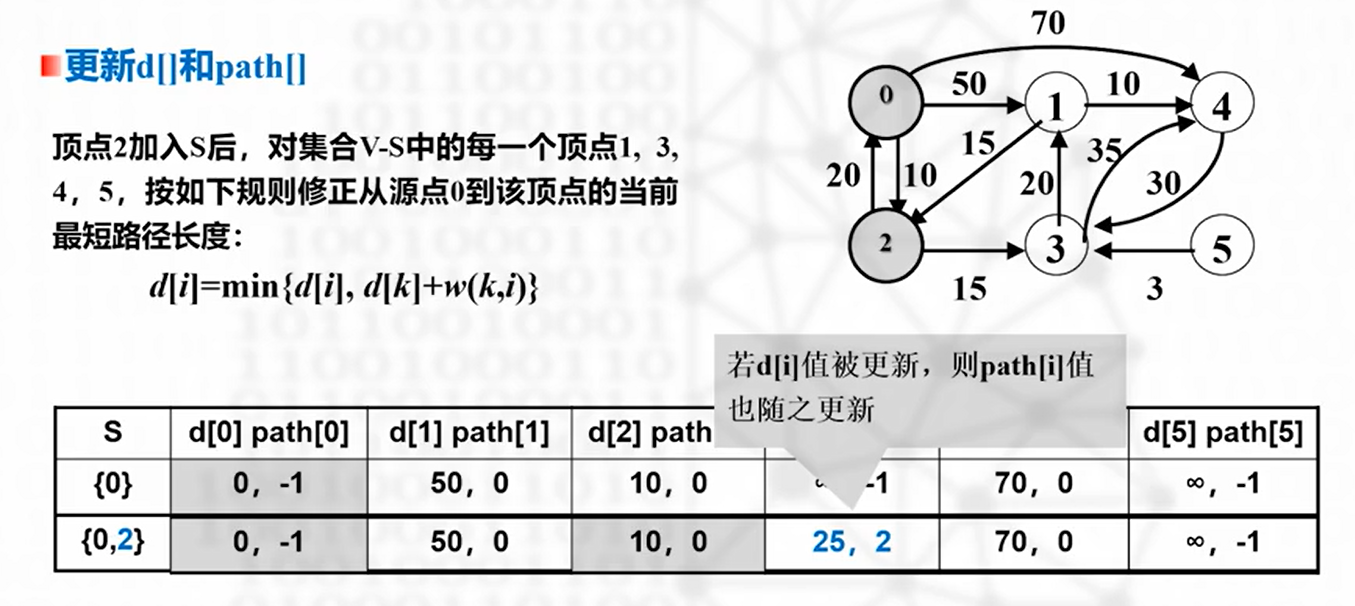
数据结构

• 邻接表存储
• 3个一维数组
  • 顶点 v_i 是否在集合中
  • 从源点 v₀ 到 v_i 的当前最短路径长度
  • v_i 的前驱顶点

时间复杂度

n 个顶点，e 条边，有向图

O(n²)：源点到某一特定顶点/单源最短路径

O(n³)：任意两对顶点之间的最短路径